Một con lắc lò xo dao động điều hòa theo phương ngang trên mặt phẳng không ma sát như Hình 1, có vận tốc tức thời cho bởi v(t) = 4 cos t, trong đó t tính bằng giây và v(t) tính bằng centimét/giây. Tại thời điểm t = 0, con lắc đó ở vị trí cân bằng.
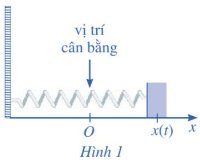
Phương trình chuyển động của con lắc đó được xác định bằng cách nào?