Diện tích hình chữ nhật thay đổi như thế nào nếu :
a) Chiều dài tăng 2 lần, chiều rộng không đổi
b) Chiều dài và chiều rộng tăng 3 lần
c) Chiều dài tăng 4 lần, chiều rộng giảm 4 lần
Diện tích hình chữ nhật thay đổi như thế nào nếu :
a) Chiều dài tăng 2 lần, chiều rộng không đổi
b) Chiều dài và chiều rộng tăng 3 lần
c) Chiều dài tăng 4 lần, chiều rộng giảm 4 lần
Một gian phòng có nền hình chữ nhật với kích thước là 4,2m và 5,4m, có một cửa sổ hình chữ nhật kích thước là 1m và 1,6m và một cửa ra vào hình chữ nhật kích thước 1,2m và 2m
Ta coi một gian phòng đạt mức chuẩn về ánh sáng nếu diện tích các cửa bằng 20% diện tích nền nhà. Hỏi gian phòng trên có đạt mức chuẩn về ánh sáng hay không ?
Thảo luận (3)Hướng dẫn giảiDiện tích nền nhà: S = 4,2.5,4 = 22,68 (m2)
Diện tích cửa sổ: S1= 1. 1,6 = 1,6 (m2).
Diện tích cửa ra vào: S2 = 1,2.2 = 2,4 (m2).
Diện tích các cửa: S' = S1+ S2 = 1,6 + 2,4 = 4 (m2).
Ta có = ≈ 17,64% < 20%
Vậy gian phòng không đạt múc chuẩn về ánh sáng.
(Trả lời bởi Tuyết Nhi Melody)
Đo cạnh (đơn vị mm) rồi tính diện tích tam giác vuông dưới đây (h.122)
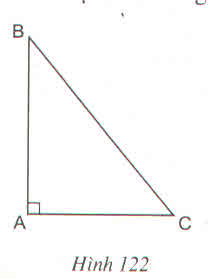
Thảo luận (2)Hướng dẫn giảiĐo hai cạnh góc vuông, ta được AB= 30mm, AC= 25mm.
Áp dụng công thức tính diện tích tam giác vuông, ta được:
S=
AB. AC =
. 30.25
Vậy S= 375mm2
(Trả lời bởi Nguyễn Đinh Huyền Mai)
ABCD là một hình vuông cạnh 12 cm, AE = x cm (h.123). Tính x sao cho diện tích tam giác ABE bằng \(\dfrac{1}{3}\) diện tích hình vuông ABCD ?
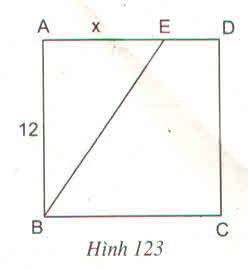
Thảo luận (1)Hướng dẫn giảiDiện tích tam giác vuông ABE là S' =
AB.AE =
.12.x = 6x
Diện tích hình vuông là S= 12.12 = 144
Theo đề bài ta có S' =
hay 6x =
Suy ra x= 8 (cm)
(Trả lời bởi Nhật Linh)
Cho một tam giác vuông. Hãy so sánh tổng diện tích của hai hình vuông dựng trên hai cạnh góc vuông với diện tích hình vuông dựng trên cạnh huyền
Gợi ý : Sử dụng định lí Py - ta - go
Thảo luận (1)Hướng dẫn giảiGiả sử tam giác vuông ABC có cạnh huyền là a và hai cạnh góc vuông là b, c (hình a).
Diện tích hình vuông dựng trên cạnh huyền a là a2
Diện tích các hình vuông dựng trên hai cạnh góc vuông b, c lần lượt là b2 + c2
Theo định lí Pitago, tam giác vuông ABC có: a2 = b2 + c2
Vậy: Trong một tam giác vuông, tổng diện tích của hai hình vuông dựng trên hai cạnh góc vuông bằng diện tích hình vuông dựng trên cạnh huyền.
Chú ý: Ta có một cách chứng minh khác đinh lyd Pitago bằng diện tích. Trên hình b, hai hình vuông ABDE và GHIK cùng có cạnh bằng b + c.
Do đó
SABDE = (b+c)2= Sb+ Sc+ 4.
(1)
SGHIK= (b+c)2 = Sa + 4.
(2)
Từ (1) và (2) suy ra
Sb+ Sc = Sa
(Trả lời bởi Tuyết Nhi Melody)
Cắt hai tam giác vuông bằng nhau từ một tấm bìa. Hãy ghép hai tam giác đó để tạo thành :
a) Một tam giác cân
b) Một hình chữ nhật
c) Một hình bình hành
Diện tích của các hình này có bằng nhau không ? Vì sao ?
Thảo luận (2)Hướng dẫn giảiCắt hai tam giác vuông bằng nhau từ một tấm bìa, chẳng hạn ta được hai hình sau:
Ghép hai tam giác trên để tạo thành:
(Trả lời bởi Tuyết Nhi Melody)
Tính diện tích các hình dưới đây (h.124) (mỗi ô vuông là một đơn vị diện tích)

Thảo luận (2)Hướng dẫn giảiDiện tích hình a là 6 ô vuông
Diện tích hình b ∆ADH = ∆ BCI nên diện tích hình b sẽ bằng diện tích hình a (ABIH).
Vậy diện tích hình b là 6 ô vuông
Diện tích hình c: ∆ KLN = ∆ NMO nên diện tích hình c sẽ bằng diện tích hình a (KMCB).
Vậy diện tích hình c là 6 ô vuông
(Trả lời bởi Nhật Linh)
Cho hình 125:
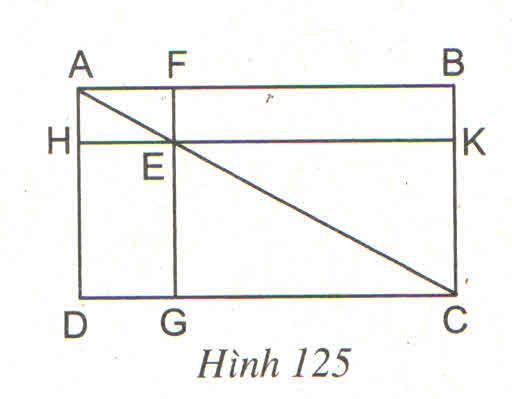
Trong đó ABCD là hình chữ nhật, E là một điểm bất kì nằm trên đường chéo AC, FG // AD và HK // AB
Chứng minh rằng hai hình chữ nhật EFBK và EGDH có cùng diện tích ?
Thảo luận (2)Hướng dẫn giải
Xem hình 125 ta thấy:
SABC = SADC
SAFE = SAHE
SEKC = SEGC
Suy ra: SABC – SAFE – SEKC = SADC – SAHE - SEGC
hay SEFBK = SEGDH
(Trả lời bởi Tuyết Nhi Melody)
Một đám đất hình chữ nhật dài 700m, rộng 400m. Hãy tính diện tích đám đất đó theo đơn vị \(m^2,km^2,a,ha\) ?
Thảo luận (2)Hướng dẫn giảiDiện tích đám đất theo đơn vị m2 là:
S = 700.400 = 280000 ( m2)
Ta có 1km2 = 1000000 ( m2)
1a = 100 (m2)
1ha = 10000 (m2)
Nên diện tích đám đất tính theo các đơn vị trên là:
S = 0,28 km2 = 2800a = 28ha
(Trả lời bởi Tuyết Nhi Melody)
Đố :
Vẽ hình chữ nhật ABCD có AB = 5cm, BC = 3cm
a) Hãy vẽ một hình chữ nhật có diện tích nhỏ hơn nhưng có chu vi lớn hơn hình chữ nhật ABCD. Vẽ được mấy hình như vậy ?
b) Hãy vẽ hình vuông có chu vi bằng chu vi hình chữ nhật ABCD. Vẽ được mấy hình vuông như vậy ? So sánh diện tích hình chữ nhật với diện tích hình vuông có cùng chu vi vừa vẽ. Tại sao trong các hình chữ nhật có cùng chu vi thì hình vuông có diện tích lớn nhất ?
Thảo luận (3)Hướng dẫn giải
a) Hình chữ nhật ABCD đã cho có diện tích là SACBD = 3.5 = 15 (cm2).
- Hình chữ nhật có kích thước 1cm x 12cm có diện tích là 12cm2 và chu vi là ( 1+12).2 = 26(cm) (có 26>15).
- Hình chữ nhật có kích thước 2cmx7cm co diện tích là 14cm2 và chu vi là (2+7).2 = 18(cm) (có 18 > 15).
Như vậy, vẽ được nhiều hình chữ nhật có diện tích bé hơn nhưng có chu vi lớn hơn hình chữ nhật ABCD cho trước.
b) Chu vi hình chữ nhật ABCD đã cho là:
(5+3).2 = 16 (cm)
Cạnh hình vuông có chu vi bằng chu vi hình chữ nhật ABCD là:
16:4 = 4(cm).
Diện tích hình vuông này là 4.4 = 16 (m2)
Vậy Shcn < Shv
Trong các hình chữ nhật có cùng chu vi thì hình vuông có diện tich lớn nhất.
Ta luôn có
≥ √ab
Suy ra ab ≤
.
Hình trên là hình vẽ chứng tỏ hình chữ nhật cạnh a,b (a>b) có diện tích nhỏ hơn diện tích hình vuông cạnh
.
Trên hình a= 5cm, b = 3cm,
= 4cm
a -
= 1cm,
- b = 1cm
Do đó
SEBCG = b. ( a-
) = 3.1 = 3 (cm2).
SDGHI =
. (
- b ) = 4.1 = 4 (cm2).
SAEGD = b.
= 3.4 = 12 (cm2).
Nên SABCD = SEBCG + SAEGD = 3 + 12 = 15(cm2).
SAEHI = SDGHI + SAEGD = 4 + 12 = 16 (cm2).
Vậy SABCD < SAEHI
Tổng quát:
Hình chữ nhật EBCG có một cạnh bằng a -
, cạnh kia bằng b.
Hình chữ nhật DGHI có một cạnh bằng
- b, cạnh kia bằng
.
Mà a -
bằng
- b và b <
( theo giả thiết a> b)
nên SEBCG < SDGHI
Cộng thêm SAEGD vào mỗi vế bất đẳng thức ta được
SEBCG + SAEGD < SDGHI + SAEGD
Vậy SABCD < SAEHI
(Trả lời bởi Nhật Linh)