Xác định đơn vị của hằng số phóng xạ λ. trong hệ SI.
Bài 17. Hiện tượng phóng xạ
Câu hỏi 5 (SGK Chân trời sáng tạo - Trang 114)
Thảo luận (1)
Câu hỏi 4 (SGK Chân trời sáng tạo - Trang 114)
Quan sát Hình 17.4, xác định những thời điểm mà số hạt của chất phóng xạ đã giảm đi và còn lại một nửa, một phần tư và một phần tám so với số hạt ban đầu.
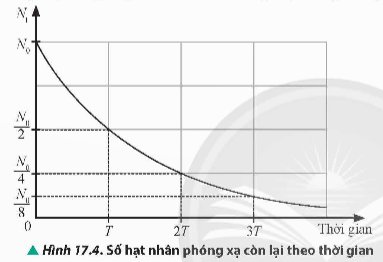
Thảo luận (1)Hướng dẫn giảiThời điểm số hạt giảm còn 1 nửa: T
Thời điểm số hạt giảm còn một phần tư: 2T
Thời điểm số hạt giảm còn một phần tám: 3T
(Trả lời bởi Nguyễn Quốc Đạt)
Bài tập 1 (SGK Chân trời sáng tạo - Trang 116)
Hiện tượng phóng xạ là hiện tượngA. một hạt nhân biến đối thành một hạt nhân khác khi hấp thụ một neutron.B. một hạt nhân không bền vững tự phát phân rã thành các hạt nhân khác và phát ra các tia phóng xạC. có thể được kiểm soát bằng cách đặt hạt nhân phóng xạ vào vùng không gian có điện trường hoặc từ trường.D. một hạt nhân phát ra các tia phóng xạ khi bị bắn phá bởi các hạt có động năng lớn.
Đọc tiếp
Hiện tượng phóng xạ là hiện tượng
A. một hạt nhân biến đối thành một hạt nhân khác khi hấp thụ một neutron.
B. một hạt nhân không bền vững tự phát phân rã thành các hạt nhân khác và phát ra các tia phóng xạ
C. có thể được kiểm soát bằng cách đặt hạt nhân phóng xạ vào vùng không gian có điện trường hoặc từ trường.
D. một hạt nhân phát ra các tia phóng xạ khi bị bắn phá bởi các hạt có động năng lớn.
Thảo luận (1)Hướng dẫn giảiHiện tượng một hạt nhân không bền vững tự phát phân rã, phát ra các tia phóng xạ và biến đổi thành một hạt nhân khác được gọi là hiện tượng phóng xạ.
Đáp án B
(Trả lời bởi Nguyễn Quốc Đạt)
Câu hỏi 6 (SGK Chân trời sáng tạo - Trang 115)
Tính độ phóng xạ của một mẫu \(^{38}_{19}K\) biết khối lượng của mẫu chất đó tại thời điểm đang xét là 10 g. Cho chu kì bán rã của \(^{38}_{19}K\) là 7,64 phút.
Thảo luận (1)Hướng dẫn giảiĐộ phóng xạ của một mẫu \({}_{19}^{38}K\)là: \(H = \lambda {N_t} = \frac{{\ln 2}}{T}.\frac{{{m_t}}}{M}.6,{022.10^{23}} = \frac{{\ln 2}}{{7,64.60}}.\frac{{10}}{{38}}.6,{022.10^{23}} = 2,{4.10^{20}}Bq\)
(Trả lời bởi Nguyễn Quốc Đạt)
Vận dụng mục 3 (SGK Chân trời sáng tạo - Trang 116)
Trình bày sơ lược về việc ứng dụng định luật phóng xạ để xác định tuổi của mẫu vật.
Thảo luận (1)Hướng dẫn giảiViệc xác định tuổi của mẫu vật bằng định luật phóng xạ có nhiều ứng dụng quan trọng trong các lĩnh vực như:
- Khảo cổ học: Xác định tuổi của các di vật khảo cổ, such as đồ gốm, công cụ đá, hóa thạch.
- Địa chất học: Xác định tuổi của các loại đá và khoáng chất, nghiên cứu lịch sử địa chất Trái Đất.
- Sinh học: Xác định tuổi của các mẫu vật sinh học, nghiên cứu quá trình tiến hóa.
- Khoa học pháp y: Xác định tuổi của các thi thể, hỗ trợ điều tra phá án.
Hạn chế:
Việc xác định tuổi của mẫu vật bằng định luật phóng xạ cũng có một số hạn chế
- Độ chính xác của phương pháp phụ thuộc vào độ chính xác của các phép đo lường và sự hiểu biết về hằng số phóng xạ của đồng vị phóng xạ được sử dụng.
- Phương pháp này chỉ áp dụng cho các mẫu vật có chứa đồng vị phóng xạ có chu kỳ bán rã phù hợp.
- Một số yếu tố môi trường có thể ảnh hưởng đến kết quả đo lường, ví dụ sự ô nhiễm phóng xạ.
(Trả lời bởi Nguyễn Quốc Đạt)
Bài tập 2 (SGK Chân trời sáng tạo - Trang 116)
Tia có khả năng đâm xuyên mạnh nhất là
A. tia α. B. tia β+.
C. tia β-. D. tia γ
Thảo luận (1)Hướng dẫn giải
Bài tập 4 (SGK Chân trời sáng tạo - Trang 116)
Một mẫu chất phóng xạ có hằng số phóng xạ λ = 0,1 s-1, ban đầu chứa 5.1012 hạt nhân chưa phân rã. Hãy xác định số hạt nhân phóng xạ đã phân rã và độ phóng xạ sau 30 giây kể từ lúc ban đầu
Thảo luận (1)Hướng dẫn giảiSố hạt nhân phóng xạ còn lại là: \({N_t} = {N_0}.{e^{ - \lambda t}} = {5.10^{12}}.{e^{ - 0,1.30}} = 2,{49.10^{11}}\)hạt
Số hạt nhân phóng xạ đã phân rã là: ∆Nt = N0 - Nt = 5.1012 - 2,49.1011 = 4,75.1012 (hạt)
Độ phóng xạ sau 30 giây là: Ht = \(\lambda \).Nt = 0,1.2,49.1011 = 2,49.1010 (Bq)
(Trả lời bởi Nguyễn Quốc Đạt)
Bài tập 5 (SGK Chân trời sáng tạo - Trang 116)
Ta có thể xác định tuổi của các mẫu vật thông qua việc đo hoạt độ phóng xạ của đồng vị \(^{14}_6C\) bên trong nó. Hãy xác định tuổi của một mẫu gỗ hóa thạch nếu tỉ số hoạt độ phóng xạ của đồng vị \(^{14}_6C\) trong mẫu gỗ hóa thạch và trong một mẫu gỗ tươi có cùng khối lượng bằng 0,63.
Thảo luận (1)Hướng dẫn giải\(\frac{{{H_t}}}{{{H_0}}} = 0,63 \Rightarrow \frac{{{N_t}}}{{{N_0}}} = 0,63 \Rightarrow \frac{{{m_t}}}{{{m_0}}} = 0,63 \Rightarrow \frac{{{m_0}{{.2}^{ - \frac{t}{T}}}}}{{{m_0}}} = 0,63\)
\( \Rightarrow {2^{ - \frac{t}{T}}} = 0,63 \Rightarrow {2^{ - \frac{t}{{5730}}}} = 0,63 \Rightarrow t = 3819,5\)(năm)
(Trả lời bởi Nguyễn Quốc Đạt)
Bài tập 3 (SGK Chân trời sáng tạo - Trang 116)
Xác định các hạt nhân ^A_ZX trong các phương trình phân rã sau:a) ^{238}_{92}Urightarrow^A_ZX+^4_2He b) ^{210}_{84}Porightarrow^{206}_{82}Pb+^A_ZXc) ^{132}_{58}Cerightarrow^A_ZX+^0_1e+v_e d) ^{135}_{54}Xerightarrow^A_ZX+^0_1e+overline{v_3}
Đọc tiếp
Xác định các hạt nhân \(^A_ZX\) trong các phương trình phân rã sau:
a) \(^{238}_{92}U\rightarrow^A_ZX+^4_2He\) b) \(^{210}_{84}Po\rightarrow^{206}_{82}Pb+^A_ZX\)
c) \(^{132}_{58}Ce\rightarrow^A_ZX+^0_1e+v_e\) d) \(^{135}_{54}Xe\rightarrow^A_ZX+^0_1e+\overline{v_3}\)
Thảo luận (1)Hướng dẫn giảia) \({}_{92}^{238}U \to {}_{90}^{234}Th + {}_2^4He\)
b) \({}_{84}^{210}Po \to {}_{82}^{206}Pb + {}_2^4He\)
c) \({}_{58}^{132}Ce \to {}_{57}^{132}La + {}_1^0e + {\nu _e}\)
d) \({}_{54}^{135}Xe \to {}_{55}^{135}Cs + {}_{ - 1}^0e + \overline {{\nu _e}} \)
(Trả lời bởi Nguyễn Quốc Đạt)
Luyện tập mục 3 (SGK Chân trời sáng tạo - Trang 116)
Tính hằng số phóng xạ của các đồng vị phóng xạ trong Bảng 17.1.
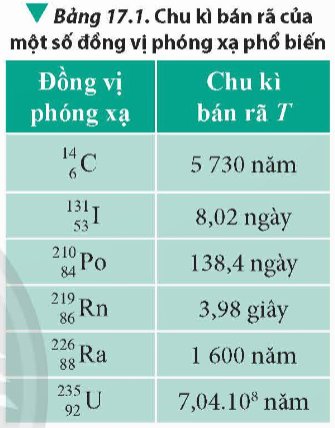
Thảo luận (1)Hướng dẫn giải\({\lambda _C} = \frac{{\ln 2}}{T} = \frac{{\ln 2}}{{5730.365.24.60.60}} = 3,{8.10^{ - 12}}{s^{ - 1}}\)
\({\lambda _I} = \frac{{\ln 2}}{T} = \frac{{\ln 2}}{{8,02.24.60.60}} = 0,{1.10^{ - 5}}{s^{ - 1}}\)
\({\lambda _{Po}} = \frac{{\ln 2}}{T} = \frac{{\ln 2}}{{138,4.24.60.60}} = 5,{7.10^{ - 8}}{s^{ - 1}}\)
\({\lambda _{Rn}} = \frac{{\ln 2}}{T} = \frac{{\ln 2}}{{3,98}} = 0,174{s^{ - 1}}\)
\({\lambda _{Ra}} = \frac{{\ln 2}}{T} = \frac{{\ln 2}}{{1600.365.24.60.60}} = 13,{7.10^{ - 12}}{s^{ - 1}}\)\({\lambda _U} = \frac{{\ln 2}}{T} = \frac{{\ln 2}}{{7,{{04.10}^8}.365.24.60.60}} = 3,{122.10^{ - 23}}{s^{ - 1}}\)
(Trả lời bởi Nguyễn Quốc Đạt)