Bạn Thanh cắt 4 hình tròn bằng giấy có bán kính lần lượt là 4 cm, 6 cm, 7 cm và 8 cm để dán trang trí trên một mảnh giấy, trên đó có vẽ trước hai đường thẳng a và b. Biết rằng a và b là hai đường thẳng song song với nhau và cách nhau một khoảng 6 cm (nghĩa là mọi điểm trên đường thẳng b đều cách a một khoảng 6 cm). Hỏi nếu bạn Thanh dán sao cho tâm của cả 4 hình tròn đều nằm trên đường thẳng b thì hình nào đè lên đường thẳng a, hình nào không đè lên đường thẳng a?
Bài 16. Vị trí tương đối của đường thẳng và đường tròn
Bài tập 5.20 (SGK Kết nối tri thức với cuộc sống - Tập 1 - Trang 103)
Bạn Thanh cắt 4 hình tròn bằng giấy có bán kính lần lượt là 4 cm, 6 cm, 7 cm và 8 cm để dán trang trí trên một mảnh giấy, trên đó có vẽ trước hai đường thẳng a và b. Biết rằng a và b là hai đường thẳng song song với nhau và cách nhau một khoảng 6 cm (nghĩa là mọi điểm trên đường thẳng b đều cách a một khoảng 6 cm). Hỏi nếu bạn Thanh dán sao cho tâm của cả 4 hình tròn đều nằm trên đường thẳng b thì hình nào đè lên đường thẳng a, hình nào không đè lên đường thẳng a?
Đọc tiếp
Thảo luận (1)
Bài tập 5.21 (SGK Kết nối tri thức với cuộc sống - Tập 1 - Trang 103)
Cho đường tròn (O) đi qua ba đỉnh A, B và C của một tam giác cân tại A, Chứng minh rằng đường thẳng đi qua A và song song với BC là một tiếp tuyến của (O).
Thảo luận (1)Hướng dẫn giải
Ta có đường thẳng AO là trục đối xứng của đường tròn.
Nên B là điểm đối xứng của C qua AO.
Gọi H là giao điểm của AO và BC.
Khi đó ta có: AH \( \bot \) BC mà d // BC nên AH \( \bot \) d.
Vậy d là một tiếp tuyến của đường tròn.
(Trả lời bởi Nguyễn Quốc Đạt)
Bài tập 5.22 (SGK Kết nối tri thức với cuộc sống - Tập 1 - Trang 103)
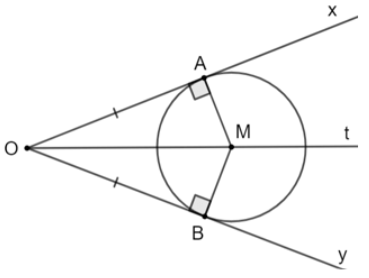
Cho góc xOy với đường phân giác Ot và điểm A trên cạnh Ox, điểm B trên cạnh Oy sao cho OA = OB. Đường thẳng qua A và vuông góc với Ox cắt Ot tại M. Chứng minh rằng OA và OB là hai tiếp tuyến cắt nhau của đường tròn (M; MA).
Thảo luận (1)Hướng dẫn giải
Ta có: OA là tiếp tuyến của đường tròn (P; PA) do OA \( \bot \) PA tại A.
Xét tam giác OAP và tam giác OBP có:
OP chung
\(\widehat {{\rm{AOP}}} = \widehat {{\rm{BOP}}}\) (do OP là tia phân giác của góc \(\widehat {{\rm{AOB}}}\))
OA = OB
Vậy \(\Delta {\rm{OAP}} = \Delta {\rm{OBP}}\) (c.g.c)
Suy ra: PA = PB (hai cạnh tương ứng)
\(\widehat {{\rm{OAP}}} = \widehat {{\rm{OBP}}} = 90^\circ \) (hai góc tương ứng) hay OB \( \bot \) PB
Do đó OA là tiếp tuyến của đường tròn (P; PA)
Vậy OA và OB là hai tiếp tuyến cắt nhau của (O).
(Trả lời bởi Nguyễn Quốc Đạt)
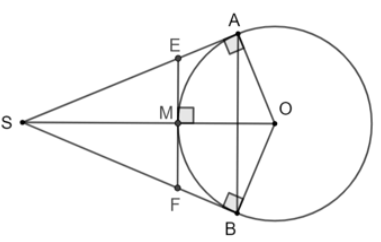
Bài tập 5.23 (SGK Kết nối tri thức với cuộc sống - Tập 1 - Trang 103)
Cho SA và SB là hai tiếp tuyến cắt nhau của đường tròn (O) (A và B là hai tiếp điểm). Gọi M là một điểm tùy ý trên cung nhỏ AB. Tiếp tuyến của (O) tại M cắt SA tại E và cắt SB tại F.
a) Chứng minh rằng chu vi của tam giác SEF bằng SA + SB.
b) Giả sử M là giao điểm của đoạn SO với đường tròn (O). Chứng minh rằng SE = SF.
Thảo luận (1)Hướng dẫn giảia)
Hai tiếp tuyến EM và EA cắt nhau tại E nên EM = EA
Hai tiếp tuyến FM và EB cắt nhau tại F nên FM = FB
\(\begin{array}{*{20}{l}}{{C_{\Delta SEF}} = SE + SF + EF}\\{\; = SE + SF + EM + MF}\\{\; = SE + EA + SF + BF}\\{\; = SA + SB}\end{array}\)
b)
SA và SB là hai tiếp tuyến cắt nhau tại S nên SO là phân giác của góc \(\widehat {{\rm{ASB}}}\).
\( \Rightarrow \widehat {{\rm{OSA}}} = \widehat {{\rm{OSB}}}\) hay \(\widehat {{\rm{MSE}}} = \widehat {{\rm{MSF}}}\)
Xét tam giác SME và tam giác SMF có:
\(\widehat {{\rm{SME}}} = \widehat {{\rm{SMF}}} = 90^\circ \)
SM chung
\(\widehat {{\rm{MSE}}} = \widehat {{\rm{MSF}}}\)
\( \Rightarrow \Delta {\rm{SME}} = \Delta {\rm{SMF}}\) (g.c.g)
\( \Rightarrow {\rm{SE}} = {\rm{SF}}\) (hai cạnh tương ứng)
(Trả lời bởi Nguyễn Quốc Đạt)