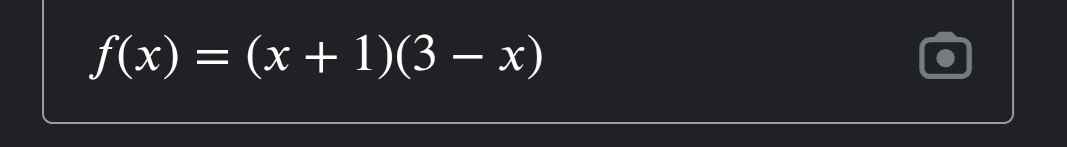\(f\left(x\right)=\left(x+1\right)\left(3-x\right)=3x-x^2+3-x\)
\(=-x^2+2x+3\)
\(\Delta'=1^2-1\cdot\left(-1\right)\cdot3=4>0,a=-1< 0\)
\(\Rightarrow f\left(x\right)\) có hai nghiệm phân biệt : \(x_1=-1,x_2=3\)
Khi đó \(f\left(x\right)>0\forall x\in\left(-\infty;-1\right)\cup\left(3;+\infty\right)\)
\(f\left(x\right)< 0\forall x\in\left(-1;3\right)\).
Giúp mik vs T^T, lập bảng xét dấu rút gọn nha :33
Xét dấu của biểu thức sau: \(\dfrac{\left(x-1\right)\left(x^2-4x+5\right)}{\left|x+3\right|}\)
giải bpt băng cách lập bảng xét dấu:
\(\frac{x+2}{3x+1}\le\frac{x-2}{2x-1}\)
giải bất phương trình sau : \(\frac{-3x+1}{2x+1}\le-2\)
giải bằng xét dấu nhị thức bậc nhất .
Giúp tui bài tập này với :
Lập bảng xét dấu các biểu thức :
\(C=\dfrac{\left(x^2-1\right)\left(x-1\right)}{\left(2x-5\right)\left(3-x\right)}\)
giải bất phương trình : \(\frac{x+2}{3x+1}\)<= \(\frac{x-2}{2x-1}\)
giải bằng xét dấu nhị thức bậc nhất
giải bất phương trình : \(\frac{x+2}{3x+1}\) <= \(\frac{x-2}{2x-1}\)
giải bằng xét dấu nhị thức bậc nhất
giải bất phương trình : \(\frac{x+2}{3x+1}\) <= \(\frac{x-2}{2x-1}\)
giải bằng xét dấu nhị thức bậc nhất
giải bất phương trình : \(\frac{x+2}{3x+1}\)<= \(\frac{x-2}{2x-1}\)
giải bằng xét dấu nhị thức bậc nhất
giải bất phương trình : \(\frac{x+2}{3x+1}\) <= \(\frac{x-2}{2x-1}\)
giải bằng xét dấu nhị thức bậc nhất
