Ôn tập chương Đường thẳng vuông góc. Đường thẳng song song
Các câu hỏi tương tự
Vẽ a//b vẽ b//c
Hãy viết giả thiết và kết luận của hình vẽ trên
a và c có song song với nhau không vì sao
(Yêu cầu HS viết giả thiết, kết luận) Cho góc vuông xOy, điểm A thuộc tia Ox. Kẻ tia Az vuông góc với Ox sao cho tia Az nằm trong góc xOy.a) Chứng minh Oy // Az?b) Gọi An là tia phân giác của góc xAz, Om là tia phân giác của góc xOy. Chứng minh Om//An.c) Kẻ AH vuông góc với Om (H thuộc Om). Tính số đo góc OAH? Mn giúp mik với ak. Cảm ơn nhiều
Đọc tiếp
(Yêu cầu HS viết giả thiết, kết luận)
Cho góc vuông xOy, điểm A thuộc tia Ox. Kẻ tia Az vuông góc với Ox sao cho tia Az nằm trong góc xOy.
a) Chứng minh Oy // Az?
b) Gọi An là tia phân giác của góc xAz, Om là tia phân giác của góc xOy. Chứng minh Om//An.
c) Kẻ AH vuông góc với Om (H thuộc Om). Tính số đo góc OAH?
Mn giúp mik với ak. Cảm ơn nhiều
Vẽ hình, ghi giả thiết, kết luận và chứng minh các định lý sau :
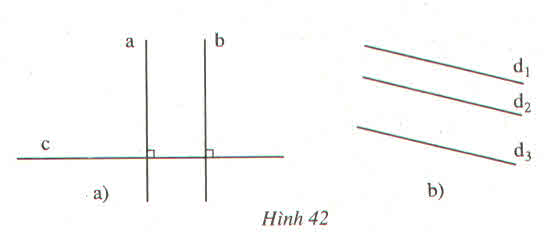
a ) Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau .
b ) Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị bằng nhau.
c ) Nếu hai góc nhọn xOy và x'O'y' có Ox // O'x' ; Oy // O'y' thì xOy = X'O'y'
Cho hình vẽ dưới đây: M x A 40 độ B t C N y 50 độ a) Chứng minh: Ax // Cyb) Từ B kẻ tia Bt nằm trong góc ABC sao cho Bt // Cy. Tính số đo góc CBt.c) Chứng minh ABperp BC.Mọi người làm nhanh hộ mik mik cảm ơn mik đang cần gấp!!!!!
Đọc tiếp
Cho hình vẽ dưới đây:
a) Chứng minh: Ax // Cy
b) Từ B kẻ tia Bt nằm trong góc ABC sao cho Bt // Cy. Tính số đo góc CBt.
c) Chứng minh \(AB\perp BC\).
Mọi người làm nhanh hộ mik mik cảm ơn mik đang cần gấp!!!!!
a) Biết Ax//By
C/m:widehat{AOB}widehat{xAO}+widehat{yBO}
b) Biết widehat{AOB}widehat{xAO}+widehat{yBO}
C/m:Ax//By
A x B y O
Đọc tiếp
a) Biết \(Ax//By\)
\(C/m:\widehat{AOB}=\widehat{xAO}+\widehat{yBO}\)
b) Biết \(\widehat{AOB}=\widehat{xAO}+\widehat{yBO}\)
\(\)\(C/m:Ax//By\)
Bài 1 Cho ΔABC có AB 1/2AC. Gọi M là trung điểm của BC. Kẻ Ax là phân giác góc ngoài tại đỉnh A của ΔABC. Qua M kẻ MH ⊥ Ax (H∈Ax). Tia MH cắt AB tại E và cắt AC tại F. a) CMR: AEAFb) Qua B kẻ tia By// AC, By cắt MH tại I. CMR: BEBIc) CMR: BECFd) CMR: CFBFBài 2 Cho ΔABC có ABAC và đường phân giác AD (D∈BC). Trên tia AC lấy điểm E sao cho AEAB.a) CMR: BDDEb) Gọi K là giao điểm của AB và ED. CMR: ΔDBK Δ DECc) ΔABC cần có thêm điều kiện gì để điểm D cách đều 3 cạnh của ΔAKC
Đọc tiếp
Bài 1 Cho ΔABC có AB< 1/2AC. Gọi M là trung điểm của BC. Kẻ Ax là phân giác góc ngoài tại đỉnh A của ΔABC. Qua M kẻ MH ⊥ Ax (H∈Ax). Tia MH cắt AB tại E và cắt AC tại F.
a) CMR: AE=AF
b) Qua B kẻ tia By// AC, By cắt MH tại I. CMR: BE=BI
c) CMR: BE=CF
d) CMR: CF>BF
Bài 2 Cho ΔABC có AB<AC và đường phân giác AD (D∈BC). Trên tia AC lấy điểm E sao cho AE=AB.
a) CMR: BD=DE
b) Gọi K là giao điểm của AB và ED. CMR: ΔDBK= Δ DEC
c) ΔABC cần có thêm điều kiện gì để điểm D cách đều 3 cạnh của ΔAKC
Cho định lí : Nếu một đường thẳng cắt hai đường thẳng phân biệt và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì các góc đồng vị bằng nhau.
- Hãy cho biết giả thiết của định lí đó.
- Hãy cho biết kết luận của định lí đó.
- Hãy chứng minh định lí đó.
Hãy phát biểu các định lí được diễn tả bằng các hình vẽ sau, rồi viết giả thiết, kết luận của từng định lí (xem bài 5)
Bài 2:Ta có:
xÂO=300, AÔB= 1000 và OBy= 1100
Chứng minh: xx’ // yy’.










