a) Ta có phương trình 3x - y = 2 (1)
Vì (1) \(\Leftrightarrow\left\{{}\begin{matrix}x\in R\\y=3x-2\end{matrix}\right.\)
+ Vẽ đưởng thẳng biểu diễn tập nghiệm của phương trình:
Với y = 3x - 2
Cho x = 0 => y = -2 được A(0; 2).
Cho y = 0 => 3x = 2 => x = ta được B(
; 0).
Biều diễn cặp số A(0; 2) và B(; 0) trên hệ trục tọa độ và đường thẳng AB chính là tập nghiệm của phương trình 3x - y = 2.
b) x + 5y = 3 \(\Leftrightarrow\left\{{}\begin{matrix}x=-5y+3\\y\in R\end{matrix}\right.\)
Ta được nghiệm tổng quát của phương trình là (-5y + 3, y)
Hay \(\left\{{}\begin{matrix}x=-5y+3\\y\in R\end{matrix}\right.\)
Biểu diễn hình học: tập nghiệm là đường thẳng AB với A(3; 0) B(-2; 1).
\(4x-3y=-1\Leftrightarrow\left\{{}\begin{matrix}x\in R\\3y=4x+1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\in R\\y=\dfrac{4}{3}x+\dfrac{1}{3}\end{matrix}\right.\)
Tập nghiệm là đường thẳng qua A (0; \(\dfrac{1}{3}\)) và B (\(\dfrac{-1}{4}\); 0)

d) \(x+5y=0\Leftrightarrow\left\{{}\begin{matrix}x=-5y\\y\in R\end{matrix}\right.\)
Tập nghiệm là đường thẳng qua O(0; 0) và A(-5; 1).
e) \(4x+0y=-2\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{-1}{2}\\y\in R\end{matrix}\right.\)
Tập nghiệm là đường thẳng x = \(\dfrac{-1}{2}\), qua A(\(\dfrac{-1}{2}\); 0) và song song với trục tung.
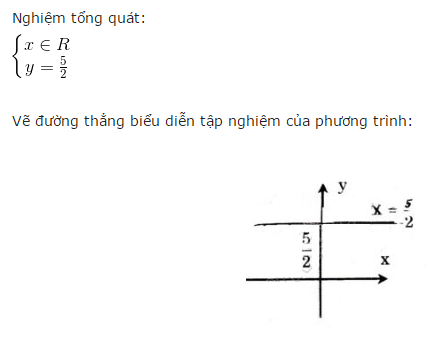
f) \(0x+2y=5\Leftrightarrow\left\{{}\begin{matrix}x\in R\\y=\dfrac{5}{2}\end{matrix}\right.\)