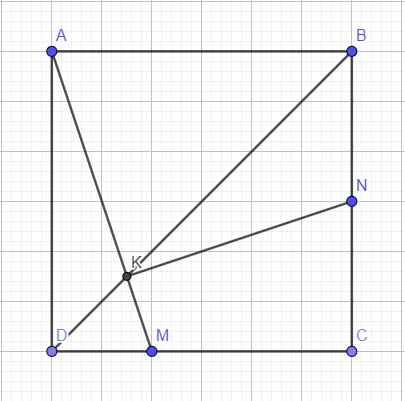
Trên hệ trục tọa độ Oxy, cho hình vuông ABCD. Gọi M là 1 điểm thuộc đoạn thẳng CD sao cho \(\overrightarrow{MC}=2.\overrightarrow{DM}\). Gọi N là trung điểm của đoạn thẳng BC và tọa độ của N là: \(N\left(0;2019\right)\).
Gọi K là giao điểm của 2 đường thẳng AM và BD. Biết đường thẳng AM có phương trình là : \(x-10y+2018=0\). Tính khoảng cách từ gốc tọa độ O đến đường thẳng NK ?
P/s: Em xin phép nhờ quý thầy cô và các bạn giúp đỡ bài toán trong đề cương của trường THPT Việt Nam -- Ba Lan ( Thành phố Hà Nội )
Talet: \(\dfrac{KM}{AK}=\dfrac{DM}{AB}=\dfrac{1}{3}\Rightarrow KM=\dfrac{1}{3}AK\Rightarrow KM=\dfrac{1}{4}AM\Rightarrow\overrightarrow{KM}=\dfrac{1}{4}\overrightarrow{AM}\)
Mà \(\overrightarrow{AM}=\overrightarrow{AD}+\overrightarrow{DM}=\overrightarrow{AD}+\dfrac{1}{3}\overrightarrow{AB}\Rightarrow\overrightarrow{KM}=\dfrac{1}{4}\overrightarrow{AD}+\dfrac{1}{12}\overrightarrow{AB}\)
\(\overrightarrow{KN}=\overrightarrow{KM}+\overrightarrow{MC}+\overrightarrow{CN}=\dfrac{1}{4}\overrightarrow{AD}+\dfrac{1}{12}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AD}\)
\(=\dfrac{3}{4}\overrightarrow{AB}-\dfrac{1}{4}\overrightarrow{AD}\)
\(\Rightarrow\overrightarrow{AM}.\overrightarrow{KN}=\left(\overrightarrow{AD}+\dfrac{1}{3}\overrightarrow{AB}\right)\left(\dfrac{3}{4}\overrightarrow{AB}-\dfrac{1}{4}\overrightarrow{AD}\right)=\dfrac{1}{4}AB^2-\dfrac{1}{4}AD^2=0\)
\(\Rightarrow AM\perp KN\Rightarrow\) đường thẳng KN nhận (10;1) là 1 vtpt
Phương trình NK:
\(10\left(x-0\right)+1\left(y-2019\right)=0\Leftrightarrow10x+y-2019=0\)
\(d\left(O;NK\right)=\dfrac{\left|-2019\right|}{\sqrt{10^2+1^2}}=\dfrac{2019}{\sqrt{101}}\)