f, Ta có: \(\left\{{}\begin{matrix}\left|x+1\right|\ge0\\\left|x+2\right|\ge0\\\left|x+3\right|\ge0\end{matrix}\right.\Rightarrow\left|x+1\right|+\left|x+2\right|+\left|x+3\right|\ge0\)
\(\Rightarrow4x\ge0\Rightarrow x\ge0\)
\(\Rightarrow x+1+x+2+x+3=4x\)
\(\Rightarrow3x+6=4x\)
\(\Rightarrow x=6\)
Vậy x = 6
Không nói đề thì thôi. Tìm x luôn :-)
f) \(\left|x+1\right|+\left|x+2\right|+\left|x+3\right|=4x\)
Ta có: \(\left|x+1\right|\ge0;\left|x+2\right|\ge0;\left|x+3\right|\ge0\)
\(\Rightarrow\) \(\left|x+1\right|+\left|x+2\right|+\left|x+3\right|=x+1+x+2+x+3\)\(\Rightarrow\)\(\left|x+1\right|+\left|x+2\right|+\left|x+3\right|=3x+6\)
\(\Rightarrow3x+6=4x\Rightarrow x=6\)
Ta thấy: \(\left\{{}\begin{matrix}\left|x+1\right|\ge0\\\left|x+2\right|\ge0\\\left|x+3\right|\ge0\end{matrix}\right.\)
\(\Rightarrow\left|x+1\right|+\left|x+2\right|+\left|x+3\right|\ge0\)
\(\Rightarrow4x\ge0\Rightarrow x\ge0\)
=> x + 1 + x + 2 + x + 3 = 4x
=> 3x + 6 = 4x
=> 6 = 4x - 3x
=> x = 6
Ta có:
\(\left|x+1\right|+\left|x+2\right|+\left|x+3\right|\ge0\)
\(\Leftrightarrow4x\ge0\Rightarrow x\ge0\)
\(\Rightarrow\)x lúc này chỉ nhận kết quả dương hoặc 0 chứ không thể là số âm
\(\Leftrightarrow x+1+x+2+x+3=4x\)
\(\Leftrightarrow3x+6=4x\)
\(\Leftrightarrow x=6\)
Với mọi giá trị của \(x\in R\) ta có:
\(\left|x+1\right|\ge0;\left|x+2\right|\ge0;\left|x+3\right|\ge0\)
\(\Rightarrow\left|x+1\right|+\left|x+2\right|+\left|x+3\right|\ge0\)
mà \(\left|x+1\right|+\left|x+2\right|+\left|x+3\right|=4x\)
nên \(4x\ge0\Rightarrow x\ge0\)
\(\Rightarrow\left\{{}\begin{matrix}\left|x+1\right|=x+1\\\left|x+2\right|=x+2\\\left|x+3\right|=x+3\end{matrix}\right.\)(1)
Thay (1) vào đề bài ta có:
\(x+1+x+2+x+3=4x\)
\(\Rightarrow3x-4x=-1-2-3\)
\(\Rightarrow-x=-6\Rightarrow x=6\)
Vậy \(x=6\).
Chúc bạn học tốt!!!























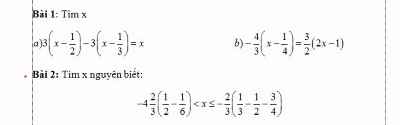 giúp mik giải 2 bài này vs ạ
giúp mik giải 2 bài này vs ạ