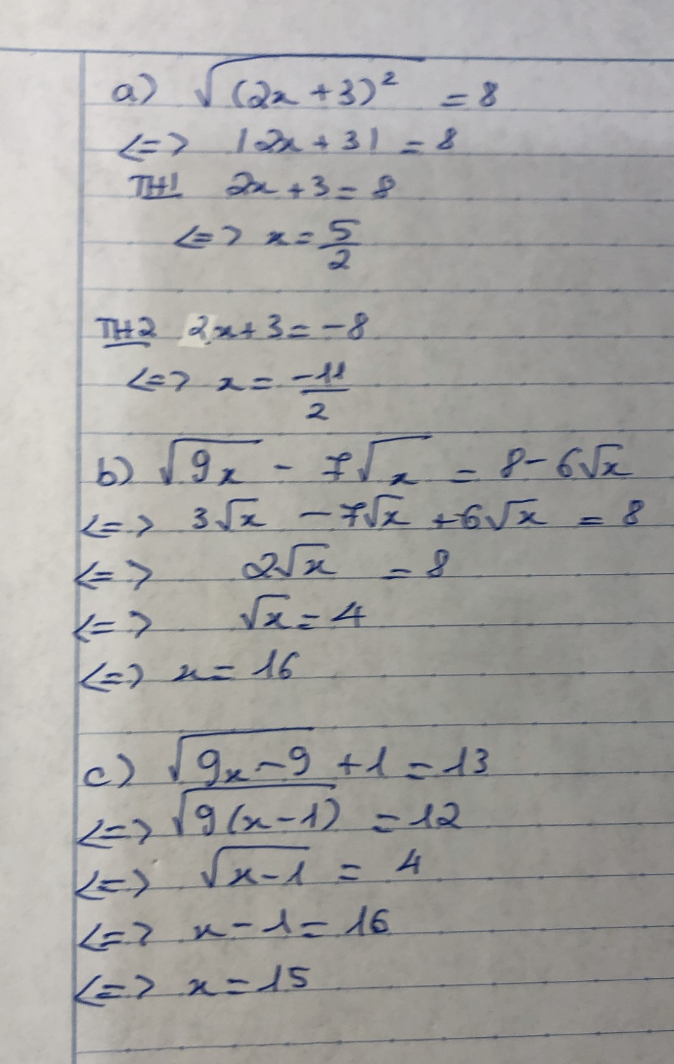Question

* Tìm x, bt:

a.\(\sqrt{\left(2x+3\right)^2}=8\)

b.\(\sqrt{9x}-7\sqrt{x}=8-6\sqrt{x}\)

c.\(\sqrt{9x-9}+1=13\)

Answer 1

a) ⇔ |2x+3| = 8
⇒ \(\left[{}\begin{matrix}2x+3=8\\2x+3=-8\end{matrix}\right.\) ⇔ \(\left[{}\begin{matrix}2x=5\\2x=-11\end{matrix}\right.\) ⇔ \(\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-\dfrac{11}{2}\end{matrix}\right.\)

Vậy...

Answer 2

Answer 3

b) ĐKXĐ: \(x\ge0\)

\(\Leftrightarrow3\sqrt{x}-7\sqrt{x}+6\sqrt{x}=8\)

\(\Leftrightarrow2\sqrt{x}=8\)

\(\Leftrightarrow\sqrt{x}=4\)

\(\Leftrightarrow x=16\) (Vì \(x\ge0\) )

Vậy x = 16

c) ĐKXĐ: \(x\ge1\)

\(\Leftrightarrow\sqrt{9\left(x-1\right)}=12\)

\(\Leftrightarrow3\sqrt{x-1}=12\)

\(\Leftrightarrow\sqrt{x-1}=4\)

\(\Leftrightarrow x-1=16\)

\(\Leftrightarrow x=17\)(TM)

Vậy x = 17

Answer 4

b) \(\sqrt{\text{9x}}-7\sqrt{x}=8-6\sqrt{x}\)   (ĐK: x≥0)

⇔ \(\text{3}\sqrt{\text{x}}-7\sqrt{x}+\text{6}\sqrt{x}=8\)

⇔ \(\sqrt{x}=4\)

⇔ \(x=16\)    (TMĐK)

Vậy x = 16

Answer 5

a)\(\Rightarrow2x+3=8\Rightarrow2x=5\Rightarrow x=\dfrac{5}{2}\)

b)\(\sqrt{9x}-7\sqrt{x}=8-6\sqrt{x}\Rightarrow3\sqrt{x}-\sqrt{x}=8\)

\(\Rightarrow2\sqrt{x}=8\Rightarrow\sqrt{x}=4\Rightarrow x=16\)

c)\(\sqrt{9x-9}+1=13\Rightarrow3\sqrt{x-1}=12\)\(\Rightarrow\sqrt{x-1}=4\Rightarrow x-1=16\Rightarrow x=17\)

Answer 6

a)\(\Rightarrow2x+3=8\Rightarrow2x=5\Rightarrow x=\dfrac{5}{2}\)

b)\(\sqrt{9x}-7\sqrt{x}=8-6\sqrt{x}\Rightarrow3\sqrt{x}-\sqrt{x}=8\)

\(\Rightarrow2\sqrt{x}=8\Rightarrow\sqrt{x}=4\Rightarrow x=16\)

c)\(\sqrt{9x-9}+1=13\Rightarrow3\sqrt{x-1}=12\)\(\Rightarrow\sqrt{x-1}=4\Rightarrow x-1=16\Rightarrow x=17\)