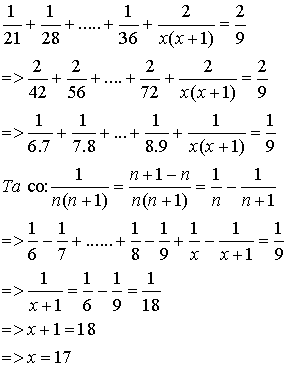Ta có : \(\dfrac{1}{21}+\dfrac{1}{28}+...+\dfrac{2}{x\left(x+1\right)}=\dfrac{2}{9}\)
\(\Rightarrow\dfrac{2}{42}+\dfrac{2}{56}+\dfrac{2}{72}+.....+\dfrac{2}{x\left(x+1\right)}\Rightarrow2\left(\dfrac{1}{42}+\dfrac{1}{56}+\dfrac{1}{72}+.....+\dfrac{1}{x\left(x+1\right)}\right)=\dfrac{2}{9}\\ \Rightarrow2\left(\dfrac{1}{6.7}+\dfrac{1}{7.8}+\dfrac{1}{8.9}+....+\dfrac{1}{x\left(x+1\right)}\right)=\dfrac{2}{9}\\ \Rightarrow2\left(\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{9}+....+\dfrac{1}{x}-\dfrac{1}{x+1}\right)=\dfrac{2}{9}\\ \Rightarrow2\left(\dfrac{1}{6}-\dfrac{1}{x+1}\right)=\dfrac{2}{9}\\ \Rightarrow\dfrac{1}{6}-\dfrac{1}{x+1}=\dfrac{2}{9}:2\\ \Rightarrow\dfrac{1}{6}-\dfrac{1}{x+1}=\dfrac{2}{9}.\dfrac{1}{2}\\ \Rightarrow\dfrac{1}{6}-\dfrac{1}{x+1}=\dfrac{1}{9}\\ \Rightarrow\dfrac{1}{x+1}=\dfrac{1}{6}-\dfrac{1}{9}\\ \Rightarrow\dfrac{1}{x+1}=\dfrac{3}{54}\\ \Rightarrow x+1=\dfrac{54}{3}\\ \Rightarrow x=\dfrac{54}{3}-1=\dfrac{51}{3}\\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \)