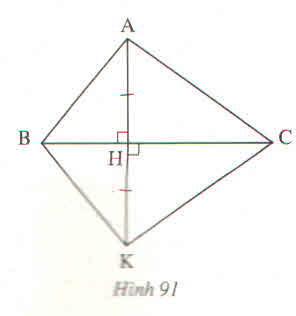
Giải:
∆AHB và ∆KBH có
AH=KH(gt)
\(\widehat{AHB}\)=\(\widehat{KHM}\)
BH cạnh chung .
nên ∆AHB=∆KBH(c.g.c)
suy ra: \(\widehat{ABH}\)=\(\widehat{KBH}\)
Vậy BH là tia phân giác của góc B.
Tương tự ∆AHC =∆KHC(c.g.c)
Suy ra: \(\widehat{ACH}\)=\(\widehat{KCH}\)
Vậy CH là tia phân giác của góc C.
- Xét ΔAHB và ΔKBH có:
BH cạnh chung
AH = KH
Nên ΔAHB = ΔKBH
Vậy BH là tia phân giác của góc B
- Tương tự ΔAHC = ΔKHC (c.g.c)
Vậy CH là tia phân giác của góc C.
Tam giác ABH và tam giác KBH có:
AH=HK(giả thuyết)
Góc AHB=góc KHB=90 độ
BH chung
Nên tam giác ABH=tam giác KBH(c-g-c)=>góc ABH=góc KBH=>BH là phân giác góc ABK
Tam giác AHC và tam giác KHC có:
AH=HK(giả thuyết)
Góc AHC=góc KHC=90 độ
HC chung
Nên tam giác AHC=tam giác KHC(c-g-c)=>Góc ACH=góc KCH=>CH là phân giác góc ACK
Vậy BH là phân giác góc ABK
CH là phân giác góc ACK