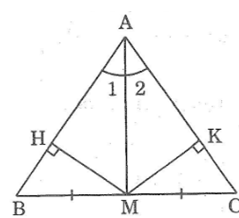
Khi một tam giác có đường trung tuyến đồng thời là đường phân giác thì đó là tam giác cân.
Ở đây tam giác ABC có AM là trung tuyến đồng thời là phân giác vậy
=> tam giác ABC là tam giác cân (tính chất tam giác cân)
Ta có hình vẽ :
Trên tia đổi của tia MA lấy điểm H sao cho MA=MH
Xét \(\Delta MBH\) và \(\Delta MCA\) có:
\(\left\{{}\begin{matrix}AM=HM\left(theocachve\right)\\\widehat{BMH}=\widehat{CMA\left(\text{đ}^2\right)}\\BM=CM\left(AMlatrungtuyen\right)\end{matrix}\right.\)
=> \(\Delta MBH\) = \(\Delta MCA\) (c.g.c)
=> +) BH=CA ( hai cạnh tương ứng) (1)
+) \(\widehat{BHM}=\widehat{CAM}\) ( hai góc tương ứng ) (2)
Ta lại có:
AM là phân giác => \(\widehat{BAM}=\widehat{MAC}\) (3)
Từ (2) và (3) suy ra: \(\widehat{BAM}=\widehat{MHB}\)
=> \(\Delta HBA\) là tam giác cân ( vì có hai góc ở đáy bằng nhau )
=> AB=HB ( hai cạnh bên của tam giác cân ) (4)
Từ (1) và (4) suy ra :
AB=AC
=> \(\Delta ABC\) là tam giác cân ( vì có hai cạnh trong tam giác bằng nhau )
( đ.p.c.m )
Kẻ MH ⊥ AB, MK ⊥ AC
Vì AM là tia phân giác của ∠(BAC) nên MH = MK (tính chất tia phân giác)
Xét hai tam giác MHB và MKC, ta có:
∠(MHB) = ∠(MKC) = 900
MH = MK (chứng minh trên)
MB = MC (gt)
Suy ra: ΔMHB = ΔMKC (cạnh huyền, cạnh góc vuông)
Suy ra: ∠B = ∠C (hai góc tương ứng)
Vậy tam giác ABC cân tại A.