Question

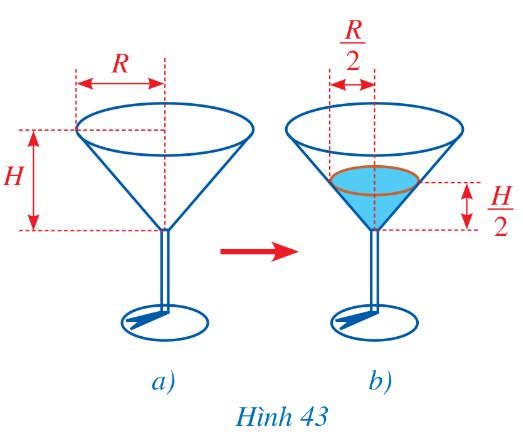
Phần đựng được nước của một chiếc ly có dạng hình nón với bán kính đáy là R và chiều cao là H (Hình 43a). Người ta đổ nước vào ly đó sao cho chiều cao của khối nước đó bằng \(\dfrac{H}{2}\) và bán kính đáy của khối nước đó bằng \(\dfrac{R}{2}\). Tính theo R và H thể tích phần không chứa nước của chiếc ly ở Hình 43b.

Answer 1

Thể tích chiếc ly là:

\(\frac{1}{3}\pi {R^2}H\) (đvtt).

Thể tích phần nước đổ vào là:

\(\frac{1}{3}\pi {\left( {\frac{R}{2}} \right)^2}\frac{H}{2} = \frac{{\pi {R^2}H}}{{24}}\) (đvtt).

Thể tích phần không chứa nước là:

\(\frac{1}{3}\pi {R^2}H - \frac{{\pi {R^2}H}}{{24}} = \frac{{7\pi {R^2}H}}{{24}}\) (đvtt).