Một người đứng ở vị trí B trên bờ sông muốn sử dụng la bàn để ước lượng khoảng cách từ vị trí đó đến một vị trí A ở trên một cù lao giữa dòng sông. Người đó đã làm như sau:
– Sử dụng la bàn, xác định được phương BA lệch với phương Nam – Bắc về hướng Đông 52°.
– Người đó di chuyển đến vị trí C, cách B một khoảng là 187 m. Sử dụng la bàn, xác định được phương CA lệch với phương Nam – Bắc về hướng Tây 27°; CB lệch với phương Nam – Bắc về hướng Tây 70° (Hình 42).
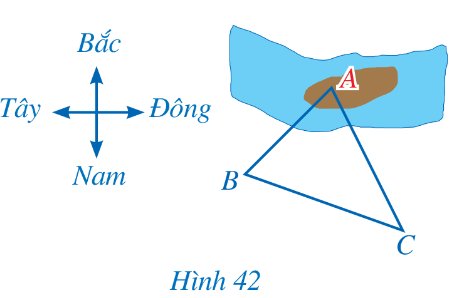
Em hãy giúp người đó tính khoảng cách AB từ những dữ liệu trên (làm tròn kết quả đến hàng đơn vị của mét).
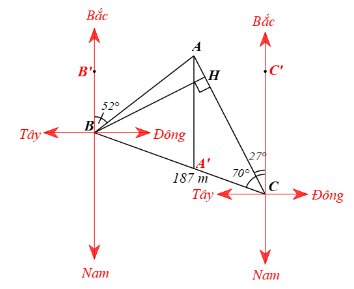
Lấy B’B, C’C là các đường thẳng biểu diễn phương Nam – Bắc như hình vẽ.
Theo bài ra ta có \(\widehat {B'BA} = 52^\circ ,\widehat {C'CA} = 27^\circ ,\widehat {C'CB} = 70^\circ \) suy ra \(\widehat {ACB} = \widehat {C'CB} - \widehat {C'CA} = 70^\circ - 27^\circ = 43^\circ \).
Kẻ AA’ ( \(A' \in BC\)) song song với phương Nam – Bắc, khi đó \(AA'//BB'//CC'\).
Vì \(AA'//BB'//CC'\) nên ta có \(\widehat {B'BA} = \widehat {BAA'} = 52^\circ \) (hai góc so le trong) và \(\widehat {A'AC} = \widehat {C'CA} = 27^\circ \) suy ra \(\widehat {BAC} = \widehat {BAA'} + \widehat {A'AC} = 52^\circ + 27^\circ = 79^\circ \).
Kẻ \(BH \bot AC\left( {H \in AC} \right)\).
Xét \(\Delta BHC\) vuông tại H có: \(\sin C = \frac{{BH}}{{BC}}\) suy ra \(BH = \sin C.BC = \sin 43^\circ .187 \approx 128\left( m \right)\).
Xét \(\Delta BAH\) vuông tại H có: \(\sin A = \frac{{BH}}{{BA}}\) suy ra \(BA = \frac{{BH}}{{\sin A}} \approx \frac{{128}}{{\sin 79^\circ }} \approx 130\left( m \right)\)
Vậy khoảng cách AB là khoảng 130m.


