Question

Một bình chứa nước có hình dạng như Hình 11. Biết rằng khi nước trong bình có chiều cao x (dm) (0 ≤ x ≤ 4) thì mặt nước là hình vuông có cạnh \(\sqrt{2+\dfrac{x^2}{4}}\) (dm). Tính dung tích của bình.

Answer 1

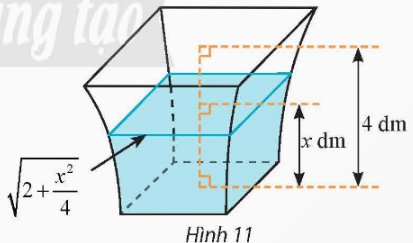
Chọn trục \(Ox\) vuông góc với mặt đáy của bình sao cho đáy nhỏ, đáy to của bình vuông góc với \(Ox\) lần lượt tại \(x = 0\) và \(x = 4\)

Diện tích mặt nước ở chiều cao \(x\) là \(S\left( x \right) = {\left( {\sqrt {2 + \frac{{{x^2}}}{4}} } \right)^2} = 2 + \frac{{{x^2}}}{4}\)

Dung tích của bình là \(V = \int\limits_0^4 {S\left( x \right)dx}  = \int\limits_0^4 {\left( {2 + \frac{{{x^2}}}{4}} \right)dx}  = \left. {\left( {2x + \frac{{{x^3}}}{{12}}} \right)} \right|_0^4 = \frac{{40}}{3}\)