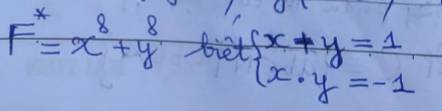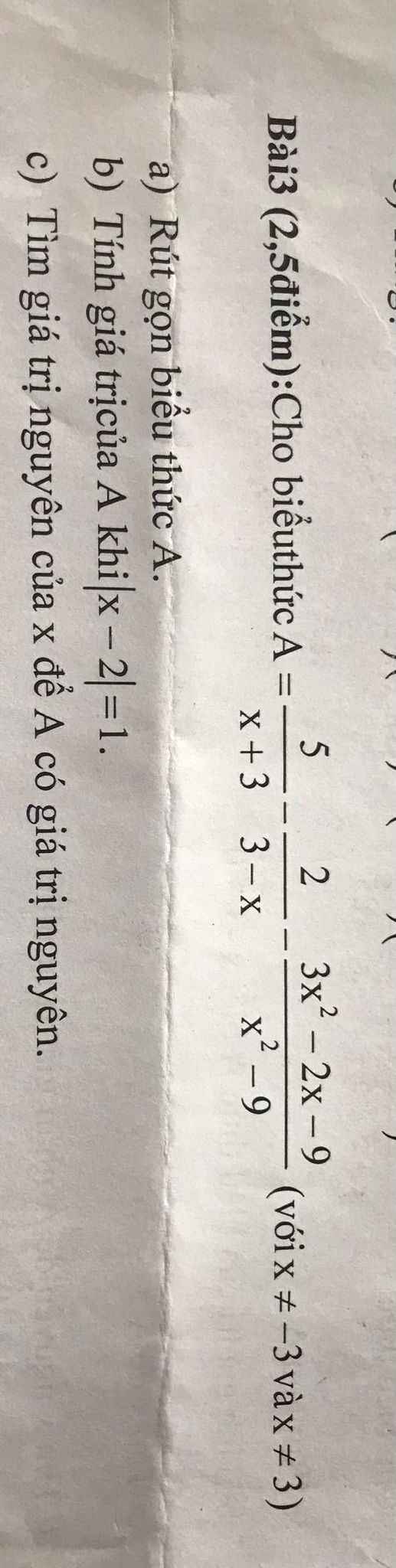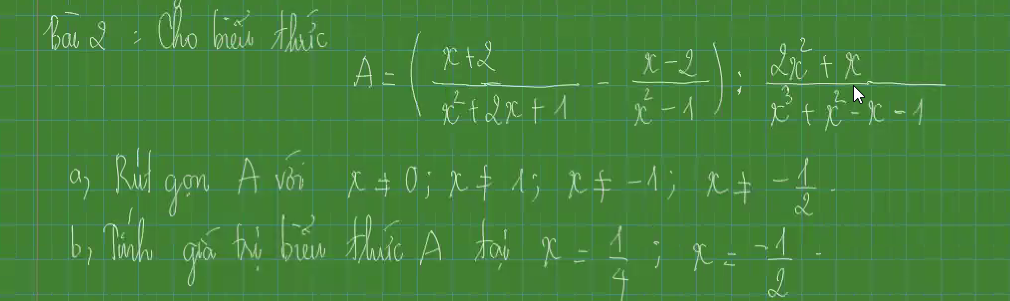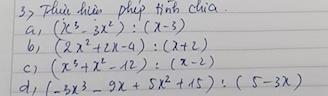Bài 4:
\(P=\dfrac{4x^2-2x+7}{2x-1}=\dfrac{2x\left(2x-1\right)+7}{2x-1}=2x+\dfrac{7}{2x-1}\in Z\\ \Leftrightarrow2x-1\inƯ\left(7\right)=\left\{-7;-1;1;7\right\}\\ \Leftrightarrow x\in\left\{-3;0;1;4\right\}\\ Q=\dfrac{4x^2-2x+3}{2x-1}=\dfrac{2x\left(2x-1\right)+3}{2x-1}=2x+\dfrac{3}{2x-1}\in Z\\ \Leftrightarrow2x-1\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\\ \Leftrightarrow x\in\left\{-1;0;1;2\right\}\)
Bài 5:
\(M=\dfrac{\left(5x-1\right)\left(5x+1\right)}{1-5x}+\dfrac{\left(y-3\right)\left(5x+1\right)}{y-3}=-\left(5x+1\right)+5x+1=0\)
Bài 6:
\(VT=\dfrac{a\left(a+3b\right)}{\left(a+3b\right)\left(a-3b\right)}-\dfrac{\left(2a+b\right)\left(a-3b\right)}{\left(a-3b\right)^2}=\dfrac{a}{a-3b}-\dfrac{2a+b}{a-3b}=\dfrac{-a-b}{a-3b}\)
\(VP=\dfrac{\left(a+b\right)\left(a+c\right)}{\left(a+c\right)\left(3b-a\right)}=\dfrac{a+b}{3b-a}=\dfrac{-a-b}{a-3b}\)
Vậy ta đc đpcm