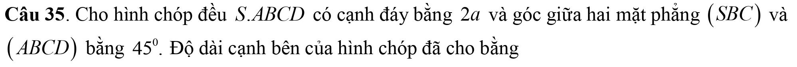Tức là câu 2, 3 của bài hình không gian đúng không em?
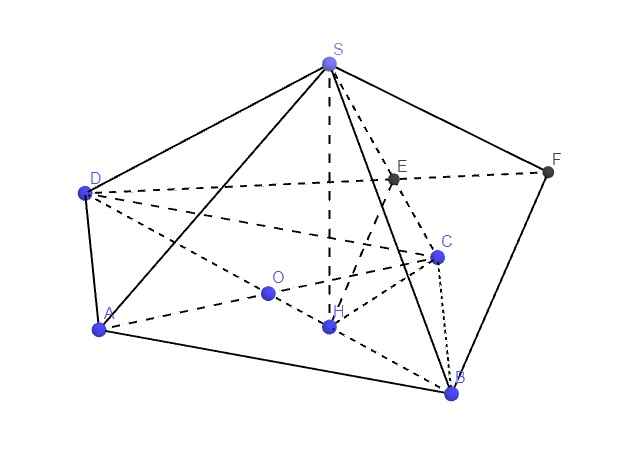
ABC là tam giác đều nên ACD cũng là tam giác đều
\(\Rightarrow OB=OD=\dfrac{AC\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
\(OH=\dfrac{1}{3}OB=\dfrac{a\sqrt{3}}{6}\Rightarrow DH=OD+OH=\dfrac{2a\sqrt{3}}{3}\)
\(SH\perp\left(ABCD\right)\Rightarrow\widehat{SDH}\) là góc giữa SD và (ABCD) \(\Rightarrow\widehat{SDH}=30^0\)
\(\Rightarrow SH=DH.tan30^0=\dfrac{2a}{3}\)
\(BH=\dfrac{2}{3}OB=\dfrac{a\sqrt{3}}{3}\Rightarrow SB=\sqrt{BH^2+SH^2}=\dfrac{a\sqrt{7}}{3}\)
c.
\(tan\widehat{HCO}=\dfrac{OH}{OC}=\dfrac{1}{\sqrt{3}}\Rightarrow\widehat{HCO}=30^0\Rightarrow\widehat{HCD}=30^0+60^0=90^0\)
Hay \(CH\perp CD\) , mà \(SH\perp\left(ABCD\right)\Rightarrow SH\perp CD\)
\(\Rightarrow CD\perp\left(SCH\right)\)
Từ H kẻ \(HE\perp SC\Rightarrow CD\perp HE\Rightarrow HE\perp\left(SCD\right)\)
Trong mp (BDE), qua B kẻ đường thẳng song song HE cắt DE kéo dài tại F
\(\Rightarrow BF\perp\left(SCD\right)\Rightarrow\widehat{BSF}\) là góc giữa SB và (SCD)
\(CH=BH=\dfrac{a\sqrt{3}}{3}\) , hệ thức lượng trong tam giác vuông SCH:
\(HE=\dfrac{SH.CH}{\sqrt{SH^2+CH^2}}=\dfrac{2a\sqrt{21}}{21}\)
Talet: \(\dfrac{HE}{BF}=\dfrac{DH}{DB}=\dfrac{2}{3}\Rightarrow BF=\dfrac{3}{2}HE=\dfrac{a\sqrt{21}}{7}\)
\(\Rightarrow sin\widehat{BSF}=\dfrac{BF}{SB}=\dfrac{3\sqrt{3}}{7}\)