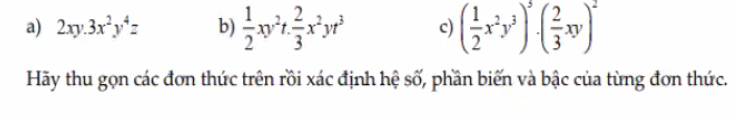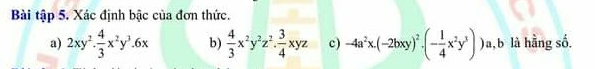Dạng 1: Nhận biết đơn thức.
Bài 1. Trong các biểu thức sau, biểu thức nào là đơn thức?
43x2yz3; 2xyz; xy.(z - 2); 21+14.y; 2012; xy23
Dạng 2: Thu gọn và xác định hệ số, phần biến, bậc của đơn thức.
a) 2x2y.3xy2
b) 2xy.45x2y3.10xyz
c) -10y2.(2xy)3.(-3x)2
Bài 3. Tính tích của các đơn thức sau rồi tìm bậc của đơn thức thu gọn.
a) 38xy2z3 và −415xyz
b) -7xyz2 và 2ay2z với a là hằng số
c) −13x2y3 và - 6 x3y4
Da...
Đọc tiếp
Dạng 1: Nhận biết đơn thức.
Bài 1. Trong các biểu thức sau, biểu thức nào là đơn thức?
43x2yz3; 2xyz; xy.(z - 2); 21+14.y; 2012; xy23
Dạng 2: Thu gọn và xác định hệ số, phần biến, bậc của đơn thức.
a) 2x2y.3xy2
b) 2xy.45x2y3.10xyz
c) -10y2.(2xy)3.(-3x)2
Bài 3. Tính tích của các đơn thức sau rồi tìm bậc của đơn thức thu gọn.
a) 38xy2z3 và −415xyz
b) -7xyz2 và 2ay2z với a là hằng số
c) −13x2y3 và - 6 x3y4
Dạng 4: Tính giá trị của đơn thức.
Tính giá trị của đơn thức −45x3y2z với x = -1, y = -2, z = - 5
HÌNH HỌC
Bài 1. Cho ∆ABC, AB = 3cm, BC = 4cm, AC = 6cm. Hỏi ∆ABC có góc nào lớn nhất?Góc nào nhỏ nhất?
Bài 2. Cho ∆ABC có AB < AC, AD là tia phân giác của góc BAC (D ∈ BC).
Chứng minh rằng:
a) góc ADB < góc ADC; b) CD>DB.
Bài 3. Cho ΔABC có AB+AC=10cm, AC−AB=4cm. So sánh góc B và góc C?
Bài 4. Cho ∆ABC vuông tại A. M là trung điểm của AC. Trên tia đối của tia MB lấy điểm E sao cho ME = MB. Chứng minh rằng:
a) CE ⊥ AC và BC > CE;
b) góc ABM > góc MBC