Bài 2:
a) Ta có: \(2012\cdot2018=\left(2015-3\right)\left(2015+3\right)=2015^2-9\)
mà \(2015\cdot2015=2015^2\)
nên \(2015\cdot2015>2012\cdot2018\)
Bài 3:
a) Ta có: \(A=\dfrac{5}{1\cdot4}+\dfrac{5}{4\cdot7}+\dfrac{5}{7\cdot10}+...+\dfrac{5}{31\cdot34}\)
\(=\dfrac{5}{3}\cdot\left(\dfrac{3}{1\cdot4}+\dfrac{3}{4\cdot7}+\dfrac{3}{7\cdot10}+...+\dfrac{3}{31\cdot34}\right)\)
\(=\dfrac{5}{3}\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{31}-\dfrac{1}{34}\right)\)
\(=\dfrac{5}{3}\left(1-\dfrac{1}{34}\right)\)
\(=\dfrac{5}{3}\cdot\dfrac{33}{34}=\dfrac{55}{34}\)
Bài 2:
a) \(2015.2015\) và \(2012.2018\)
Ta có:
\(2015.2015=2015^2\)
\(2012.2018\)
\(=\left(2015-3\right).\left(2015+3\right)\)
\(=2015^2-9\)
Vì \(2015^2>2015^2-9\) nên \(2015.2015>2012.2018\)
Bài 3:
\(A=\dfrac{5}{1.4}+\dfrac{5}{4.7}+\dfrac{5}{7.10}+...+\dfrac{5}{31.34}\)
\(A=\dfrac{5}{3}.\left(\dfrac{3}{1.4}+\dfrac{3}{4.7}+\dfrac{3}{7.10}+...+\dfrac{3}{31.34}\right)\)
\(A=\dfrac{5}{3}.\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{31}-\dfrac{1}{34}\right)\)
\(A=\dfrac{5}{3}.\left(1-\dfrac{1}{34}\right)\)
\(A=\dfrac{5}{3}.\dfrac{33}{34}\)
\(A=\dfrac{55}{34}\)
\(B=\left(1-\dfrac{1}{2}\right).\left(1-\dfrac{1}{3}\right).\left(1-\dfrac{1}{4}\right).....\left(1-\dfrac{1}{2021}\right).4042\)
\(B=\dfrac{1}{2}.\dfrac{2}{3}.\dfrac{3}{4}.....\dfrac{2020}{2021}.4042\)
\(B=\dfrac{1.2.3.....2020}{2.3.4.....2021}.4042\)
\(B=\dfrac{1}{2021}.4042\)
\(B=2\)
Bài 2:
b) \(\dfrac{353535}{676767}\) và \(\dfrac{34}{69}\)
\(\dfrac{353535}{676767}=\dfrac{35}{67}=\dfrac{35.34}{67.34}=\dfrac{1190}{2278}\)
\(\dfrac{34}{69}=\dfrac{34.35}{69.35}=\dfrac{1190}{2415}\)
Vì \(\dfrac{1190}{2278}>\dfrac{1190}{2415}\) nên \(\dfrac{353535}{676767}>\dfrac{34}{69}\)


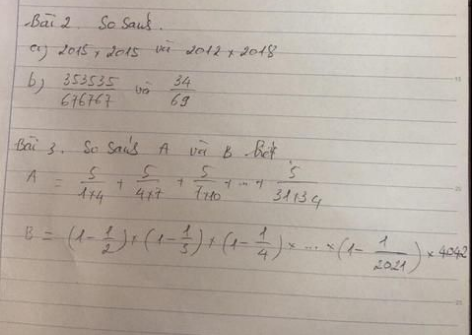 mk cần gấp . cảm ơn bạn đã giúp
mk cần gấp . cảm ơn bạn đã giúp











