\(a,=\dfrac{\sqrt{2}\left(1+\sqrt{2}\right)}{1+\sqrt{2}}=\sqrt{2}\\ b,=\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}=\sqrt{5}\\ c,=\dfrac{\sqrt{3}\left(1-\sqrt{2}\right)}{2\left(\sqrt{2}-1\right)}=-\dfrac{\sqrt{3}}{2}\\ d,=\dfrac{\sqrt{5}\left(1-\sqrt{2}\right)}{\sqrt{3}\left(1-\sqrt{2}\right)}=\dfrac{\sqrt{5}}{\sqrt{3}}=\dfrac{\sqrt{15}}{3}\\ e,=\dfrac{\sqrt{7}\left(\sqrt{7}+1\right)}{\sqrt{7}+1}=\sqrt{7}\\ f,=\dfrac{\sqrt{5}\left(\sqrt{5}+1\right)}{\sqrt{5}+1}=\sqrt{5}\\ g,=\dfrac{\sqrt{2}\left(\sqrt{5}-1\right)}{\sqrt{5}-1}=\sqrt{2}\\ h,=\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}=\sqrt{5}\)
Bài 8: Rút gọn biểu thức chứa căn bậc hai
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Giúp Mik làm.mấy bài mình đánh dấu bút đỏ nha mai Mik phải nộp rồi
Làm giúp mik bài 2 nha
Nhờ mn giúp mik vs ạ.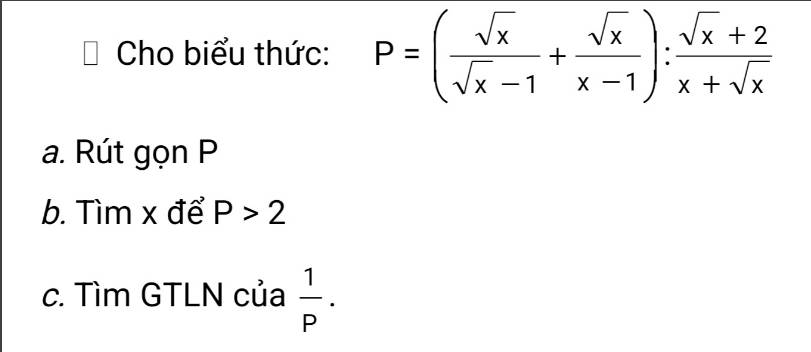
\(\left(\dfrac{x\sqrt{x}-1}{x-\sqrt{x}}-\dfrac{x\sqrt{x}+1}{x+\sqrt{x}}\right)+\left(\sqrt{x}-\dfrac{1}{\sqrt{x}}\right)\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}+\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\right)\)mik đang bí bài này mn giúp mik vs,mik cảm ơn nha
\(\dfrac{\sqrt{a+1}}{\sqrt{a^2-1}-\sqrt{a^2+a}}+\dfrac{1}{\sqrt{a-1}+\sqrt{a}}+\dfrac{\sqrt{a^3}-a}{\sqrt{a}-1}\)rut gọn giúp mik bài này nha mn,mik cảm ơn nhiều
Mn giúp mik vs ạ
Giúp mik vs mik . Thanks trc ạ
Giúp mik với, mik đang cần gấp.
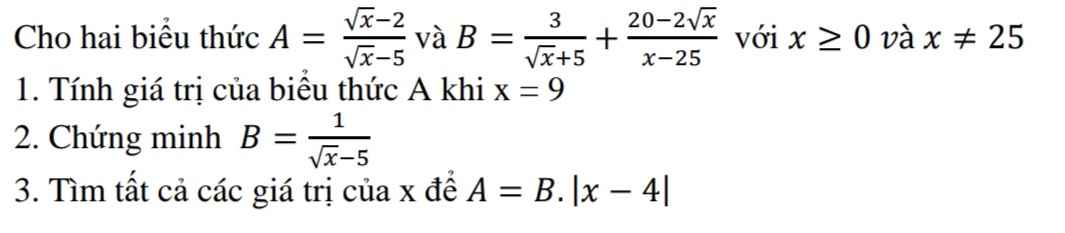
P=\(\dfrac{a+4\sqrt{a}+4}{\sqrt{a}+2}+\dfrac{4-a}{2-\sqrt{a}}\) với a>=0;a khác 4
a.Rút gọn biểu thức P
b.Tìm giá trị a sao cho P=a+1
các bạn giúp mik giải bài này trong hôm nay hoặc sáng mai nhé!:))))))))))))))))Chiều mai mik phải nộp rùi!:)))))))))))))))))))Cảm ơn các bạn nhiều!:))))))))))))))))))))))))))))))))












