Bài 7 : Bài giải
1) \(A=x^2+4x+7=x^2+2\cdot2x+2^2+3=\left(x+2\right)^2+3\ge3\)
Dấu " = " xảy ra khi : \(\left(x+2\right)^2=0\text{ }\Rightarrow\text{ }x=-2\)
\(Min_A=3\) khi x = - 2
2) \(B=4x^2+4x+6=\left(2x\right)^2+2\cdot2x+1+5=\left(2x+1\right)^2+5\ge5\)
Dấu " = " xảy ra khi \(\left(2x+1\right)^2=0\text{ }\Rightarrow\text{ }x=-\frac{1}{2}\)
\(Min_B=5\text{ khi }x=-\frac{1}{2}\)
3) \(C=x^2+x+1=x^2+x+\frac{1}{2}\cdot\frac{1}{2}+\frac{3}{4}=\left(x+\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}\)
Dấu " = " xảy ra khi \(\left(x+\frac{1}{2}\right)^2=0\text{ }\Rightarrow\text{ }x=-\frac{1}{2}\)
\(Min_C=\frac{3}{4}\text{ khi }x=-\frac{1}{2}\)








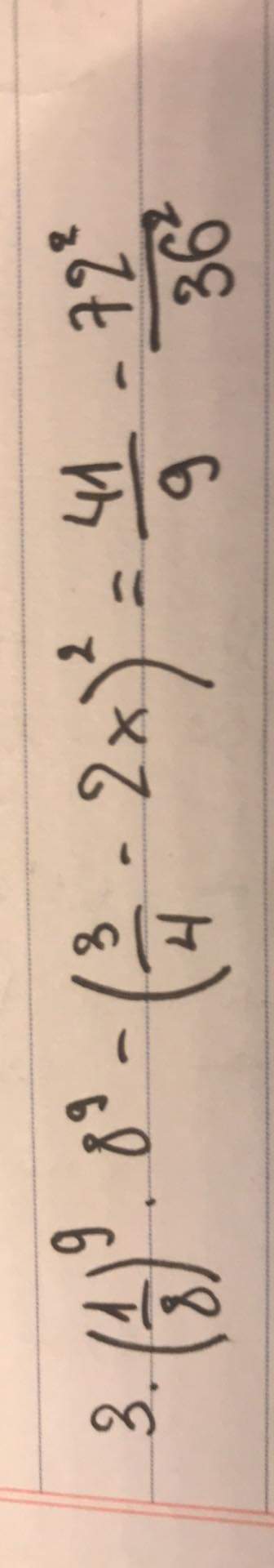



 bài 2 câu 1,2,3,5,9
bài 2 câu 1,2,3,5,9