Bài 2: Định lý đảo và hệ quả của định lý Talet
Các câu hỏi tương tự
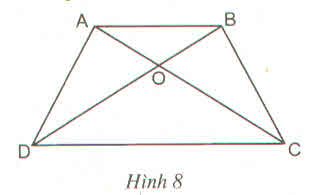
Cho hình thang ABCD( AB//CD; AB<CD) . Hai đường chéo cắt
nhau tại O.
a) CMR: OA.OD=OB.OC
b) Đường thẳng đi qua O mà song song với CD cắt AD và BC lần lượt
tại M và N. CMR: OM=ON.
c) AD cắt BC tại E. EO cắt AB và CD lần lượt tại P và Q. CMR: P là
trung điểm của AB; Q là trung điểm của CD;
mg giúp mình câu c với
Cho hình thang ABCD (AB // CD), các đường chéo cắt nhau tại O. Chứng minh; OA.OD = OB. OC
Cho hình thang ABCD(AB//CD). Gọi O là giao điểm của hai đường chéo AC và BD.
a) Tính CD,Chứng minh rằng OA.OD = OB.OC.
b) Đường thẳng qua O vuông góc với AB và CD theo thứ tự tại H và K.Tính\(\frac{OH}{OK}\)
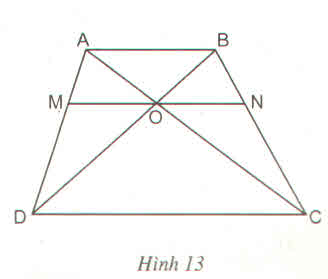
Hình thang ABCD (AB //CD) có hai đường chéo AC và BD cắt nhau tại O. Đường thẳng qua O và song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự tại M, N. Chứng minh rằng OM = ON (h.13)
Cho hình thang ABCD (AB // CD) có O là giao điểm của hai đường chéo AC và BD. Qua A, kẻ đường thẳng song song với BC cắt BD tại E. Qua B, kẻ đường thẳng song song với AD cắt AC tại F.
a) Chứng minh: EF // CD.
b) Chứng minh: AB2 = CD . EF
Hình thang ABCD ( AB // CD) O là giao điểm của AB và BD
a. CM: OA.OD = OB.OC
b. Đường thẳng qua ) song song với AB và CD cắt AD và Bc tại M và N. CM: ON = OM
Cho hình thang ABCD (AB //CD). Đường thẳng song song với đáy AB cắt các cạnh bên và các đường chéo AD, BD, AC và BC theo thứ tự tại các điểm M, N, P, Q chứng minh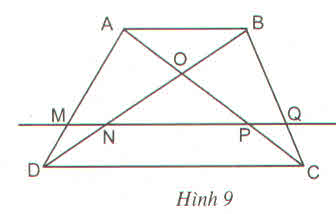 
DN\BD=CP\AC
Hình thang ABCD (AB//CD) có hai đường chéo cắt nhau tại O. Gọi M, K, N, H lần lượt là chân đường vuông góc hạ từ O xuống các cạnh AB, BC, CD, DA. Chứng minh rằng :
a) \(\dfrac{OM}{ON}=\dfrac{AB}{CD}\)
b)* \(\dfrac{OH}{OK}=\dfrac{BC}{AD}\)
: Cho hình thang ABCD (AB < CD và AB // CD). Vẽ qua A đường thẳng AK song song với BC (K DC) và AK cắt BD tại E, vẽ qua B đường thẳng BI song song với AD (I CD) cắt AC tại F.
a) Chứng minh rằng: EF // AB
b) Chứng minh rằng: AB2 = CD.EF