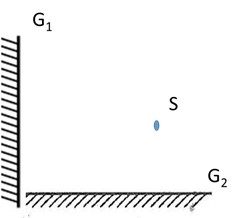
Hai gương phẳng giống nhau AB và AC được đặt hợp với nhau 1 góc 60o. Mặt phản xạ hướng vào nhau một nguồn sáng S nằm trên cạnh BC.
/a,Nêu cách vẽ đường đi của tia sáng xuất phát từ điểm S phản xạ lần lượt trên AB rồi AC rồi quay lại S
/b, gọi M,N là 1 điểm bất kì tương ứng trên AB và AC . Chứng tỏ rằng đường đi của tia sáng trong câu A là ngắn nhất

a,Cách vẽ đường đi của tia sáng phát ra từ D, phản xạ lần lượt trên AB, AC rồi quay về S. Chứng tỏ rằng độ dài đường đi đó bằng SS2:
Gọi S1 là ảnh của S qua gương AB.
S2 là ảnh của S1 qua gương AC.Do đó S1 là đối xứng của S qua AB.
S2 là đối xứng của S qua AC (như hình 6). Ta tưởng tượng rằng ta đang nằm trên “chiếc giường” AC, mắt không nhìn vào điểm sáng S mà nhìn vào gương AB. Lúc đó ta thấy tia sáng không xuất phát từ S mà dường như xuất phát từ S1 đối xứng với S qua gương AB. Tương tự như vậy, nếu đặt mắt ở S không nhìn vào gương AB mà nhìn vào gương AC, ta sẽ thấy tia sáng không xuất phát từ S1mà dường như xuất phát từ S2 đối xứng với S1 qua gương AC. Từ đó suy ra cách vẽ các tia cần tìm.
b,
b,
Chứng tỏ đường đi của tia sáng trong câu a) không lớn hơn chu vi tam giác SMN.
Chọn M ∈ AB ; N ∈ AC.
Nối SM, MN, NS.
Ta phải so sánh chu vi tam giác SMN với chu vi tam giác SIJ. Hay ta so sánh chu vi tam giác SMN với chiều dài SS2.
Dễ thấy: SM = S1M => SM + MN = S1M + MN ≥ S1N.
Mà S1N= S2N => SM + MN ≥ S2N.
=> SM + MN + NS ≥ S2N + NS ≥ SS2
=> độ dài đường đi SS2 ≤ SM + MN + NS ≡ (chu vi ∆SMN) (đpcm)
Dấu “=” xảy ra khi và chỉ khi M ≡ I và N ≡ Jthui nha
Vậy ...