a) Xét ΔABC , ta có:
AB^2=6^2=36cm
BC^2=8^2=64cm
=> AB^2+BC^2=36+64 = 100
AC^2=10^2=100cm
hay AB^2+BC^2=AC^2
=>ΔABC là tam giác vuông tại B (định lí Pytago đảo)
b) xét ΔABD và ΔAHD,ta có: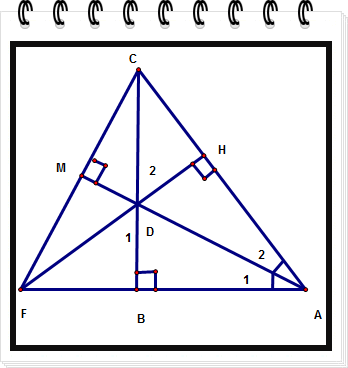
AD cạnh chung
^HAD=^BAD(AD là tia phân giác góc A)
^AHD=^ABD=90^0
=>ΔABD= ΔAHD(ch-gn)
=>AH=AB(2 cạnh tương ứng)
xét ΔAHB,ta có:
AH=AB = 8 cm(cmt)
=>ΔAHB là tam giác cân tại A.
c) tính FH :
Xét ΔDBF và ΔDHC, ta có :
^FBD = ^CHD = 90^0 (gt)
^D1 = ^D2 (đối đỉnh)
BD = HD (ΔABD=ΔAHD)
=> ΔDBF = ΔDHC
=> BF = HC
Mà : AB = AH
=>BF + AB = HC + AH
Vậy : AF = AC = 10 cm.
Xét ΔAHF vuông tại H, theo Pitago có :
FA^2 = AH^2 + HF^2
100 = 64 + HF^2
=> HF^2 = 36
=>HF^2 = 6cm
Xét ΔACF, ta có :
CB _|_ AF tại B => CB là đường cao thứ 1
FH _|_ AC tại H => FH là đường cao thứ 2
Mà CB cắt FH tại D
=> D là trực tâm (1)
Mà : AM _|_ CF tại M => AM là đường cao thứ 3 (2)
Từ (1), (2), suy ra : D thuộc đường cao AM
Vậy : A, D, M thẳng hàng

 !!!!
!!!!











 các bạn giúp mình nha!
các bạn giúp mình nha!


 Giúp mình nha các bạn
Giúp mình nha các bạn