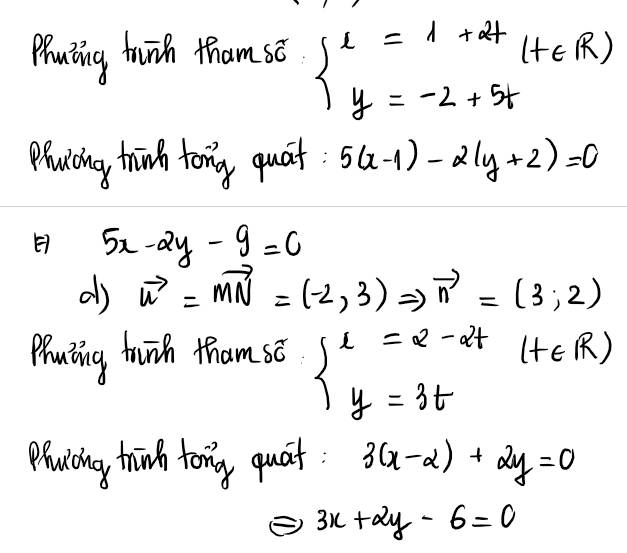Lời giải:
a
VTPT: $(-2,5)$
PTĐT $(\Delta)$ là; $-2(x-1)+5(y-3)=0$
$\Leftrightarrow -2x+5y-13=0$
b. PTĐT $(\Delta)$ là:
$1(x-2)+4(y-1)=0\Leftrightarrow x+4y-6=0$
c.
VTCP của $(\Delta)$ là: $\overrightarrow{AB}=(2,5)$
$\Rightarrow$ VTPT của $(\Delta)$ là: $(-5,2)$
PTĐT $(\Delta)$ là: $-5(x-1)+2(y+2)=0$
$\Leftrightarrow -5x+2y+9=0$
d.
Làm tương tự câu c, PT $3x+2y-6=0$
a.
d có vtcp là (5;2) nên cũng nhận (2;-5) là 1 vtpt
Phương trình tham số của d: \(\left\{{}\begin{matrix}x=1+5t\\y=3+2t\end{matrix}\right.\)
Phương trình tổng quát của d:
\(2\left(x-1\right)-5\left(y-3\right)=0\Leftrightarrow2x-5y+13=0\)
b.
d có vtpt là (1;4) nên nhận (4;-1) là 1 vtcp
Phương trình tham số d: \(\left\{{}\begin{matrix}x=2+4t\\y=1-t\end{matrix}\right.\)
Phương trình tổng quát d: \(1\left(x-2\right)+4\left(y-1\right)=0\Leftrightarrow x+4y-6=0\)
c.
\(\overrightarrow{AB}=\left(2;5\right)\) nên d nhận (2;5) là 1 vtcp và (5;-2) là 1 vtpt
d đi qua B(3;3) nên có pt tham số: \(\left\{{}\begin{matrix}x=3+2t\\y=3+5t\end{matrix}\right.\)
Phương trình tổng quát:
\(5\left(x-3\right)-2\left(y-3\right)=0\Leftrightarrow5x-2y-9=0\)
d.
\(\overrightarrow{MN}=\left(-2;3\right)\) nên d nhận (-2;3) là vtcp và (3;2) là vtpt
Phương trình tham số: \(\left\{{}\begin{matrix}x=2-2t\\y=3t\end{matrix}\right.\)
Pt tổng quát: \(3\left(x-2\right)+2\left(y-0\right)=0\Leftrightarrow3x+2y-6=0\)