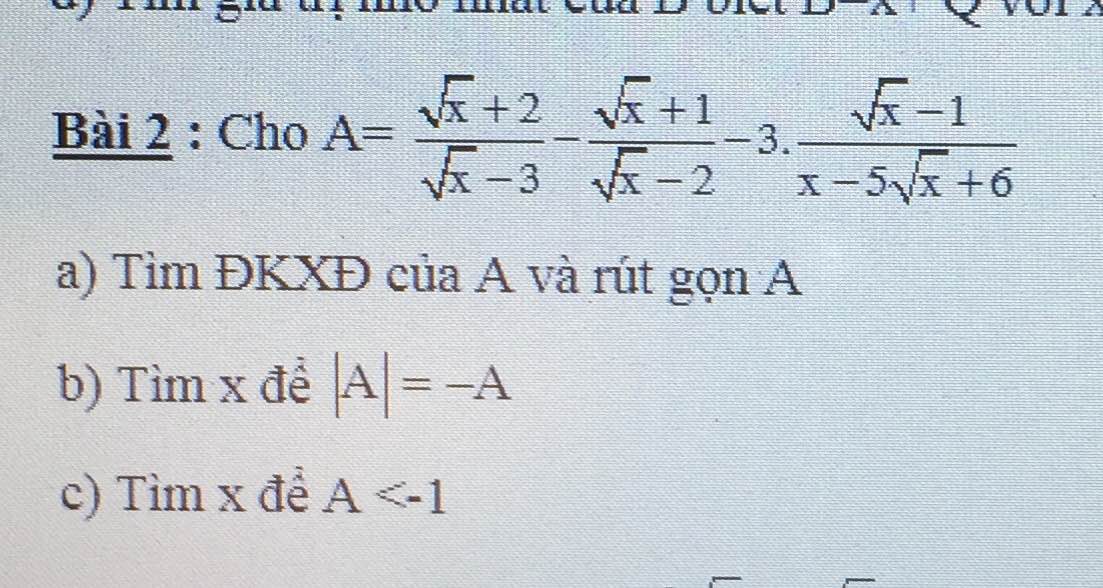\(đ\text{k}:\left\{{}\begin{matrix}\sqrt{x}-3\ne0\\x\ge0\\\sqrt{x}-2\ne0\\x-5\sqrt{x}+6\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne9\\x\ne4\\x\ge0\\\end{matrix}\right.\)
\(\Leftrightarrow A=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)-\left(\sqrt{x}+1\right)\left(\sqrt{x}-3\right)-3\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}=\dfrac{x-4-x+2\sqrt{x}+3-3\sqrt{x}+3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}=\dfrac{-\sqrt{x}+2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}=\dfrac{-1}{\sqrt{x}-3}\)
\(b,\left|A\right|=-A\Leftrightarrow\dfrac{-1}{\sqrt{x}-3}< 0\Leftrightarrow\sqrt{x}-3>0\Leftrightarrow x>9\)
\(c,A< -1\Rightarrow\dfrac{-1}{\sqrt{x}-3}+1< 0\Leftrightarrow\dfrac{\sqrt{x}-3-1}{\sqrt{x}-3}< 0\Leftrightarrow\dfrac{\sqrt{x}-4}{\sqrt{x}-3}< 0\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}\sqrt{x}-4>0\\\sqrt{x}-3< 0\end{matrix}\right.\\\left\{{}\begin{matrix}\sqrt{x}-4< 0\\\sqrt{x}-3>0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x>16\\x< 9\end{matrix}\right.\\\left\{{}\begin{matrix}x< 16\\x>9\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow9< x< 16\)