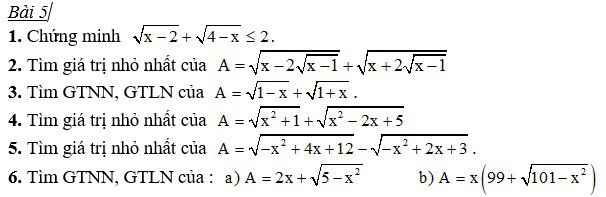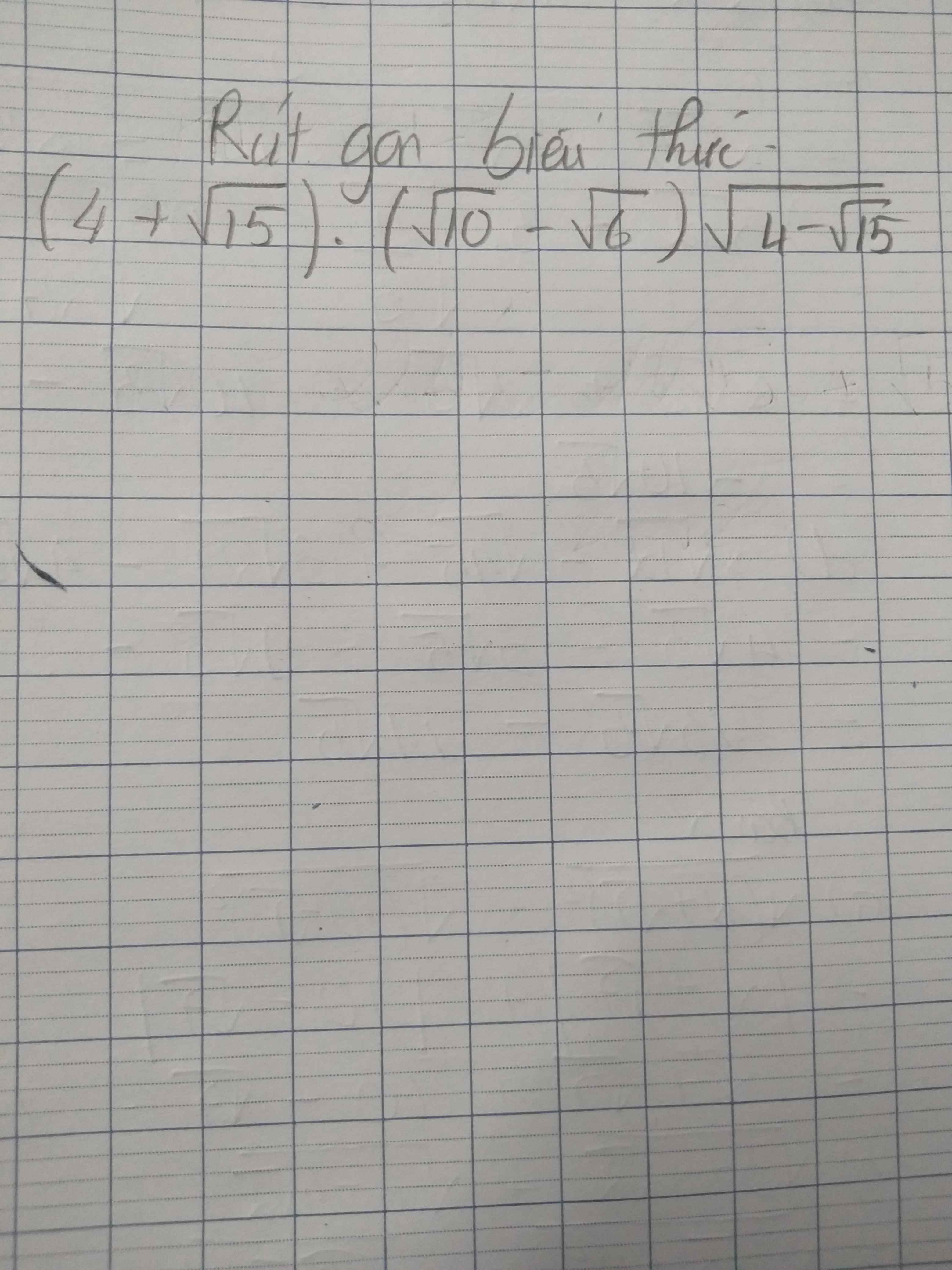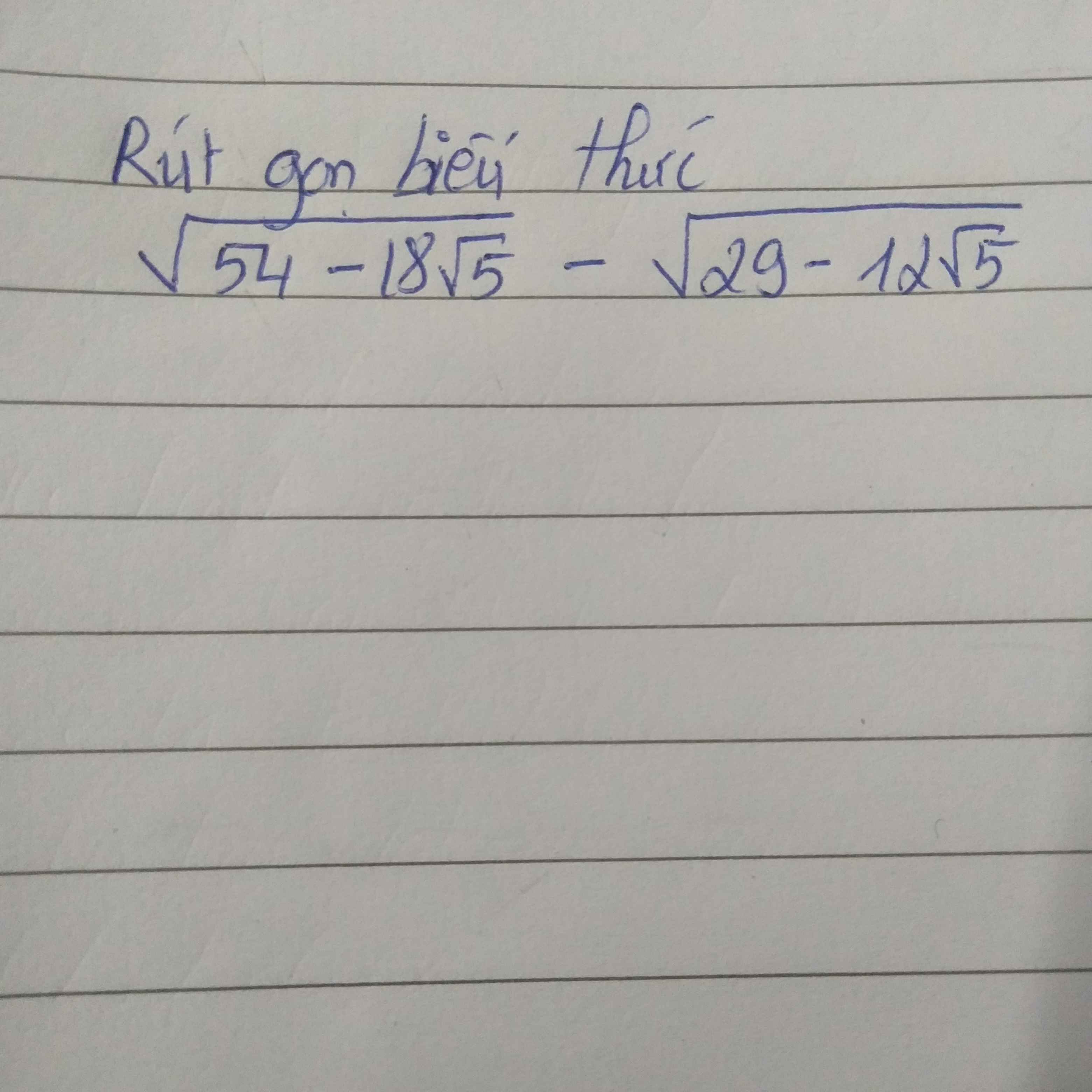Bài 1:
ĐKXĐ: \(2\le x\le4\)
Áp dụng BĐT Bunhiacopxki:
\(\left(1.\sqrt{x-2}+1.\sqrt{4-x}\right)^2\le\left(1^2+1^2\right)\left(x-2+4-x\right)=2.2=4\)
\(\Rightarrow\sqrt{x-2}+\sqrt{4-x}\le\sqrt{4}=2\left(đpcm\right)\)
Dấu "=" xảy ra \(\Leftrightarrow\dfrac{1}{\sqrt{x-2}}=\dfrac{1}{\sqrt{4-x}}\Leftrightarrow x-2=4-x\Leftrightarrow x=3\left(tm\right)\)
Bài 2:
ĐKXĐ: \(x\ge1\)
\(A=\sqrt{\left(\sqrt{x-1}-1\right)^2}+\sqrt{\left(\sqrt{x-1}+1\right)^2}\)
\(=\left|\sqrt{x-1}-1\right|+\left|\sqrt{x-1}+1\right|\)
\(=\left|1-\sqrt{x-1}\right|+\left|\sqrt{x-1}+1\right|\ge\left|1-\sqrt{x-1}+\sqrt{x-1}+1\right|=\left|2\right|=2\)
\(minA=2\Leftrightarrow\left(1-\sqrt{x-1}\right)\left(\sqrt{x-1}+1\right)\ge0\) \(\Leftrightarrow1\le x\le2\)