\(1,\\ a,=3x^2y-2xy^2-2xy^2=3x^2y-4xy^2\\ b,=\left(x+2\right)^2:\left(x+2\right)=x+2\\ c,=\dfrac{2}{x}\\ 2,\\ 1,\\ a,=2\left(x^2-2x+1\right)=2\left(x-1\right)^2\\ b,=\left(x-y\right)\left(x+y\right)+3\left(x-y\right)=\left(x-y\right)\left(x+y+3\right)\\ 2,\\ a,\Leftrightarrow x\left(x+5\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\\ b,\Leftrightarrow3x\left(x-1\right)+\left(x-1\right)=0\\ \Leftrightarrow\left(x-1\right)\left(3x+1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{1}{3}\end{matrix}\right.\\ 3,\\ a,ĐK:x\ne\pm1\\ b,A=\dfrac{\left(x+1\right)^2}{\left(x-1\right)\left(x+1\right)}=\dfrac{x+1}{x-1}\\ c,A=2\Leftrightarrow\dfrac{x+1}{x-1}=2\Leftrightarrow x+1=2x-2\Leftrightarrow x=3\left(tm\right)\)
Phép nhân và phép chia các đa thức
Đúng 1
Bình luận (0)
Các câu hỏi tương tự
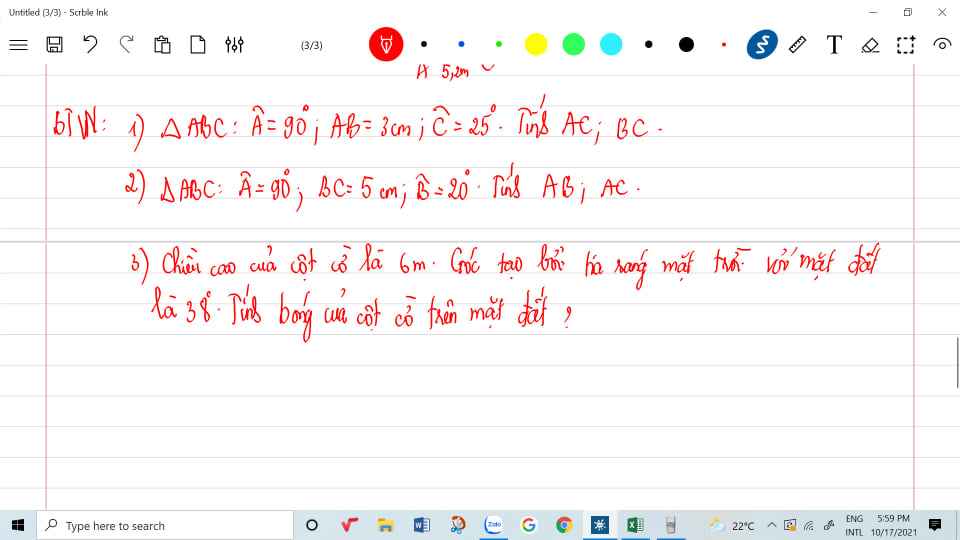 Giúp mình với ạ mình cần gấp
Giúp mình với ạ mình cần gấp
làm giúp mình câu này với ạ,mình đang cần gấp
Đọc tiếp
làm giúp mình câu này với ạ,mình đang cần gấp
m.ng ơii giải giúp mình với ạ mình cần gấp!!! Tính giá trị của đơn thức sau : a) 2x^2 y tại x = -1 , y = 1/4
b) -1/2 x^3 y^2 tại x = -1/2 , y = -4
Giúp em với,em thật sự cần gấp lắm ạ 😢
https://drive.google.com/file/d/1fK3KmBtxcctJZ_nKYrbr29KqtpezKhYV/view
giúp mình với mình cần gấp
Giúp em với please, em thật sự đang cần gấp lắm ạ 😢😭😭😭😭
giúp với mình cần gấp, 5h30 phải nộp rồi
Giúp mình với mình cần gấp kết quả ạ 1, (x²y + 6x) . (x² - 3xy) a, x⁴y - 3x³y² + 6x³ - 18x²y b, x²y - x³y² + 6x³ - 18x²y C,x⁴y - 3x³y² + 6x³ + 18x²y d, x⁴y + 3x³y² - 6x³ - 18x²y 2, Tìm x biết x . (2x - 4) - 2x² + 9x - 7 = 3 a, x = 1 b, x = 2 C, x = 3 d, x = 4 3, tính giá trị của biểu thức sau tại x = 3 ; y=2 7x . (x² - 2y) + 3xy - 7x³ a, 24 b, -4 c, 6 d, -24 Cảm ơn đã giúp đỡ mình ✨
Cho tam giác ABC tù tại A. 3 đường cao AA1, BB1,CC1 giao nhau tại H. Cm : A1H/AA1-B1H/BB1-C1H/CC1 = 1
CÁC BẠN GIÚP MK VỚI Ạ. MK CẦN GẤP















