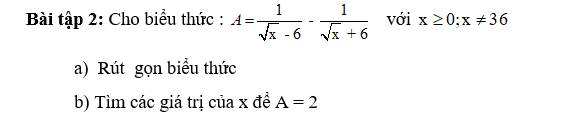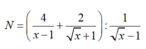1.
ĐKXĐ: \(x\ge-\dfrac{1}{4}\)
\(\sqrt{x+2}+\sqrt{4x+1}=5\)
\(\Leftrightarrow\sqrt{x+2}-2+\sqrt{4x+1}-3=0\)
\(\Leftrightarrow\dfrac{x-2}{\sqrt{x+2}+2}+\dfrac{4\left(x-2\right)}{\sqrt{4x+1}+3}=0\)
\(\Leftrightarrow\left(x-2\right)\left(\dfrac{1}{\sqrt{x+2}+2}+\dfrac{4}{\sqrt{4x+1}+3}\right)=0\)
\(\Leftrightarrow x-2=0\) (do \(\dfrac{1}{\sqrt{x+2}+2}+\dfrac{4}{\sqrt{4x+1}+3}>0\))
\(\Leftrightarrow x=2\)
2.
\(\Leftrightarrow10x^2-5x-3-\sqrt{6x^2-3x+1}=0\)
\(\Leftrightarrow5\left(2x^2-x\right)-3-\sqrt{6x^2-3x+1}=0\)
Đặt \(\sqrt{6x^2-3x+1}=t>0\)
\(\Rightarrow6x^2-3x+1=t^2\Rightarrow3\left(2x^2-x\right)=t^2-1\)
\(\Rightarrow2x^2-x=\dfrac{t^2-1}{3}\)
Phương trình trở thành:
\(5.\dfrac{t^2-1}{3}-3-t=0\)
\(\Leftrightarrow5t^2-3t-14=0\Rightarrow\left[{}\begin{matrix}t=2\\t=-\dfrac{7}{5}\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow\sqrt{6x^2-3x+1}=2\)
\(\Leftrightarrow6x^2-3x+1=4\)
\(\Leftrightarrow2x^2-x-1=0\Rightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{1}{2}\end{matrix}\right.\)
3.
ĐKXĐ: \(0\le x\le1\)
Đặt \(\sqrt{x-x^2}=t\ge0\) ta được:
\(t^2=4+3t\Leftrightarrow t^2-3t-4=0\)
\(\Rightarrow\left[{}\begin{matrix}t=-1\left(loại\right)\\t=4\end{matrix}\right.\)
\(\Rightarrow\sqrt{x-x^2}=4\)
\(\Leftrightarrow x-x^2=16\)
\(\Leftrightarrow x^2-x+16=0\) (vô nghiệm)
Vậy pt đã cho vô nghiệm
4.
ĐKXĐ: \(\left[{}\begin{matrix}x=-1\\x\ge1\end{matrix}\right.\)
- Với \(x=-1\) là 1 nghiệm của pt đã cho
- Với \(x\ge1\)
\(\sqrt{\left(x+1\right)\left(x-1\right)}+\sqrt{\left(3x+1\right)\left(x+1\right)}=2\sqrt{x+1}\)
\(\Leftrightarrow\sqrt{x-1}+\sqrt{3x+1}=2\)
\(\Leftrightarrow\sqrt{x-1}+\sqrt{3x+1}-2=0\)
\(\Leftrightarrow\sqrt{x-1}+\dfrac{3\left(x-1\right)}{\sqrt{3x+1}+2}=0\)
\(\Leftrightarrow\sqrt{x-1}\left(1+\dfrac{3\sqrt{x-1}}{\sqrt{3x+1}+2}\right)=0\)
\(\Leftrightarrow\sqrt{x-1}=0\) (do \(1+\dfrac{3\sqrt{x-1}}{\sqrt{3x+1}+2}>0\))
\(\Leftrightarrow x=1\)
Vậy tập nghiệm của pt là \(S=\left\{-1;1\right\}\)
5.
ĐKXĐ: \(x\ge1\)
\(\sqrt{x^2+x-2}+15=3\sqrt{x-1}+5\sqrt{x+2}\)
\(\Leftrightarrow\sqrt{\left(x-1\right)\left(x+2\right)}-3\sqrt{x-1}+15-5\sqrt{x+2}=0\)
\(\Leftrightarrow\sqrt{x-1}\left(\sqrt{x+2}-3\right)-5\left(\sqrt{x+2}-3\right)=0\)
\(\Leftrightarrow\left(\sqrt{x-1}-5\right)\left(\sqrt{x+2}-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x-1}=5\\\sqrt{x+2}=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=25\\x+2=9\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=26\\x=7\end{matrix}\right.\)
6.
ĐKXĐ: \(-2\le x\le2\)
\(3\left(\sqrt{2+x}-2\sqrt{2-x}\right)=10-3x-4\sqrt{4-x^2}\)
Đặt \(\sqrt{2+x}-2\sqrt{2-x}=t\)
\(\Rightarrow t^2=10-3x-4\sqrt{4-x^2}\)
Phương trình trở thành:
\(3t=t^2\Rightarrow\left[{}\begin{matrix}t=3\\t=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{2+x}-2\sqrt{2-x}=0\\\sqrt{2+x}-2\sqrt{2-x}=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{2+x}=2\sqrt{2-x}\left(1\right)\\\sqrt{2+x}=2\sqrt{2-x}+3\left(2\right)\end{matrix}\right.\)
Xét (1): \(\Leftrightarrow2+x=4\left(2-x\right)\Rightarrow x=\dfrac{6}{5}\)
Xét (2): do \(x\le2\Rightarrow\sqrt{2+x}\le2\) , mà \(2\sqrt{2-x}+3\ge3>2\) nên (2) vô nghiệm
Vậy pt có nghiệm duy nhất \(x=\dfrac{6}{5}\)