giúp mình giải bài trên vs
\(\left(x-1\right)^{x+2}=\left(x-1\right)^{x+6}\)
\(\Rightarrow\left(x-1\right)^{x+2}-\left(x-1\right)^{x+6}=0\)
\(\Rightarrow\left(x-1\right)^{x+2}\left[1-\left(x-1\right)^4\right]=0\)
\(\Rightarrow\left[{}\begin{matrix}\left(x-1\right)^{x+2}=0\\1-\left(x-1\right)^4=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x-1=0\\\left(x-1\right)^4=1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x-1=\pm1\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=1\\x\in\left\{0;2\right\}\end{matrix}\right.\)
Vậy ...
\(\left(x-1\right)^{x+2}=\left(x-1\right)^{x+6}\)
\(\Rightarrow\left(x-1\right)^{x+2}-\left(x-1\right)^{x+6}=0\)
\(\Rightarrow\left(x-1\right)^{x+2}\left[1-\left(x-1\right)^4\right]=0\)
\(\Rightarrow\left[{}\begin{matrix}\left(x-1\right)^{x+2}=0\\1-\left(x-1\right)^4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x-1=0\\\left(x-1\right)^4=1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x-1=\pm1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x\in\left\{0;2\right\}\end{matrix}\right.\)
Vậy ..............
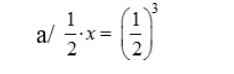giúp em bài này với ạ,giải chi tiết luôn nha,em cảm ơn
