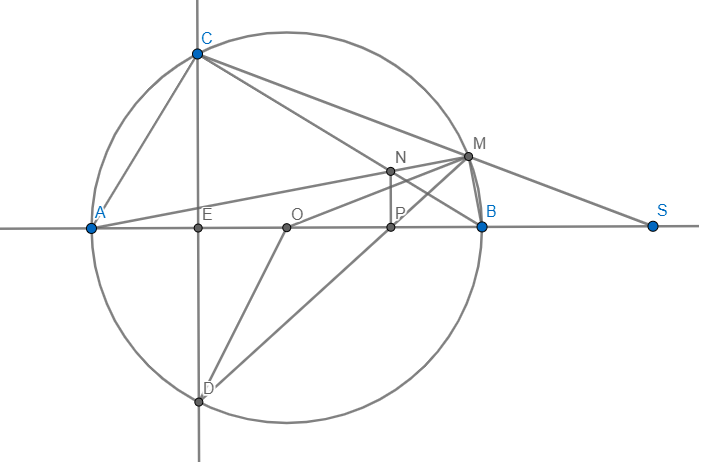
a) ACMB nội tiếp \(\Rightarrow\angle MCB=\angle MAB\)
Xét \(\Delta SMA\) và \(\Delta SBC:\) Ta có: \(\left\{{}\begin{matrix}\angle SCB=\angle SAM\\\angle ASCchung\end{matrix}\right.\)
\(\Rightarrow\Delta SMA\sim\Delta SBC\left(g-g\right)\)
b) CD cắt AB tại E
Vì AB là đường kính \(\Rightarrow\angle ACB=\angle AMB=90\)
ACMD nội tiếp \(\Rightarrow\angle AMD=\angle ACD=\angle ACE=\angle ABC\left(=90-\angle CAB\right)\)
\(\Rightarrow\angle NMP=\angle NBP\Rightarrow NMBP\) nội tiếp
mà \(\angle NMB=90\Rightarrow\angle NPB=90\Rightarrow NP\bot AB\)
mà \(CD\bot AB\Rightarrow\) \(NP\parallel CD\)
c) Vì \(\Delta OMD\) cân tại O \(\Rightarrow\angle OMP=\dfrac{180-\angle DOM}{2}=90-\dfrac{1}{2}\angle DOM\)
\(=90-\angle DCM=90-\angle ECS=\angle OSM\)
Xét \(\Delta OMP\) và \(\Delta OSM:\) Ta có: \(\left\{{}\begin{matrix}\angle OMP=\angle OSM\\\angle MOSchung\end{matrix}\right.\)
\(\Rightarrow\Delta OMP\sim\Delta OSM\left(g-g\right)\Rightarrow\dfrac{OM}{OS}=\dfrac{OP}{OM}\Rightarrow OM^2=OP.OS\)