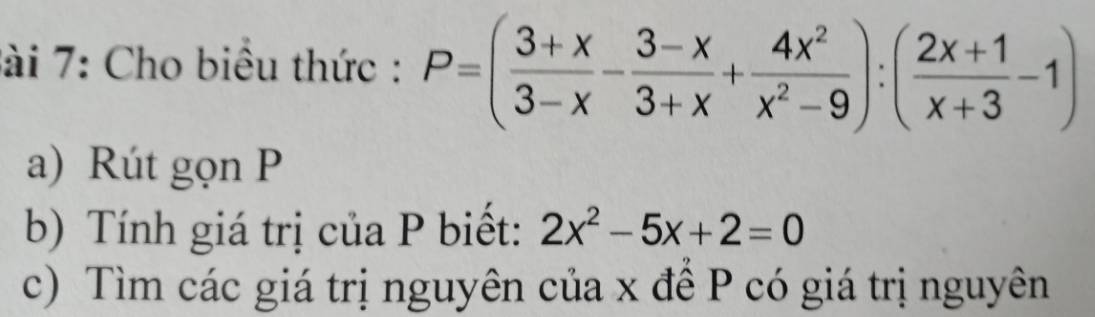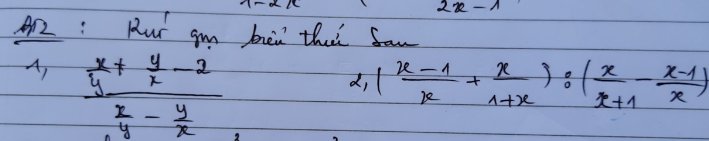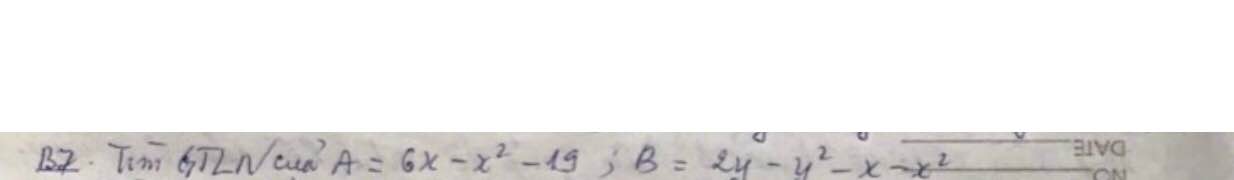Gọi hai góc ngoài tại đỉnh A,B của tứ giác ABCD là \(\widehat{A'},\widehat{B'}\).
Có: \(\widehat{A},\widehat{A'}\) là 2 góc kề bù, AM là tia phân giác của \(\widehat{A}\), \(AN\) là tia phân giác của \(\widehat{A'}\).
\(\Rightarrow\)AM⊥AN tại A.
Tương tự: BM⊥BN tại B.
Tứ giác AMBN có: \(\widehat{AMB}+\widehat{ANB}+\widehat{NAM}+\widehat{NBM}=360^0\)
\(\Rightarrow\widehat{AMB}+\widehat{ANB}+90^0+90^0=360^0\)
\(\Rightarrow\widehat{AMB}+\widehat{ANB}=180^0\left(đpcm\right)\)
Đúng 0
Bình luận (0)
