P=\(\dfrac{xy}{\sqrt{xy+xz+yz+z^2}}+\dfrac{yz}{\sqrt{yz+x^2+xy+xz}}+\dfrac{zx}{\sqrt{zx+xy+y^2+yz}}\)
\(=\dfrac{xy}{\sqrt{x+z}.\sqrt{y+z}}+\dfrac{yz}{\sqrt{x+y}.\sqrt{x+z}}+\dfrac{zx}{\sqrt{x+y}.\sqrt{y+z}}\)
\(\le\dfrac{1}{2}xy.\left(\dfrac{1}{x+z}+\dfrac{1}{y+z}\right)+\dfrac{1}{2}yz.\left(\dfrac{1}{x+y}+\dfrac{1}{x+z}\right)+\dfrac{1}{2}zx.\left(\dfrac{1}{x+y}+\dfrac{1}{y+z}\right)\)
\(=\dfrac{1}{2}\left(x+y+z\right)=1\)
Đẳng thức \(\Leftrightarrow x=y=z=\dfrac{2}{3}\)











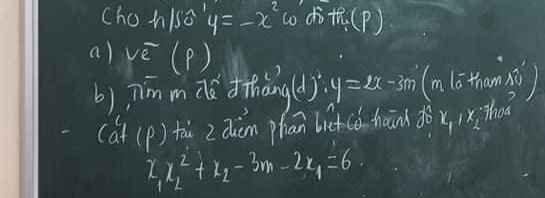







 vẽ hộ hình mik vs ạ, cám ơn!!
vẽ hộ hình mik vs ạ, cám ơn!!