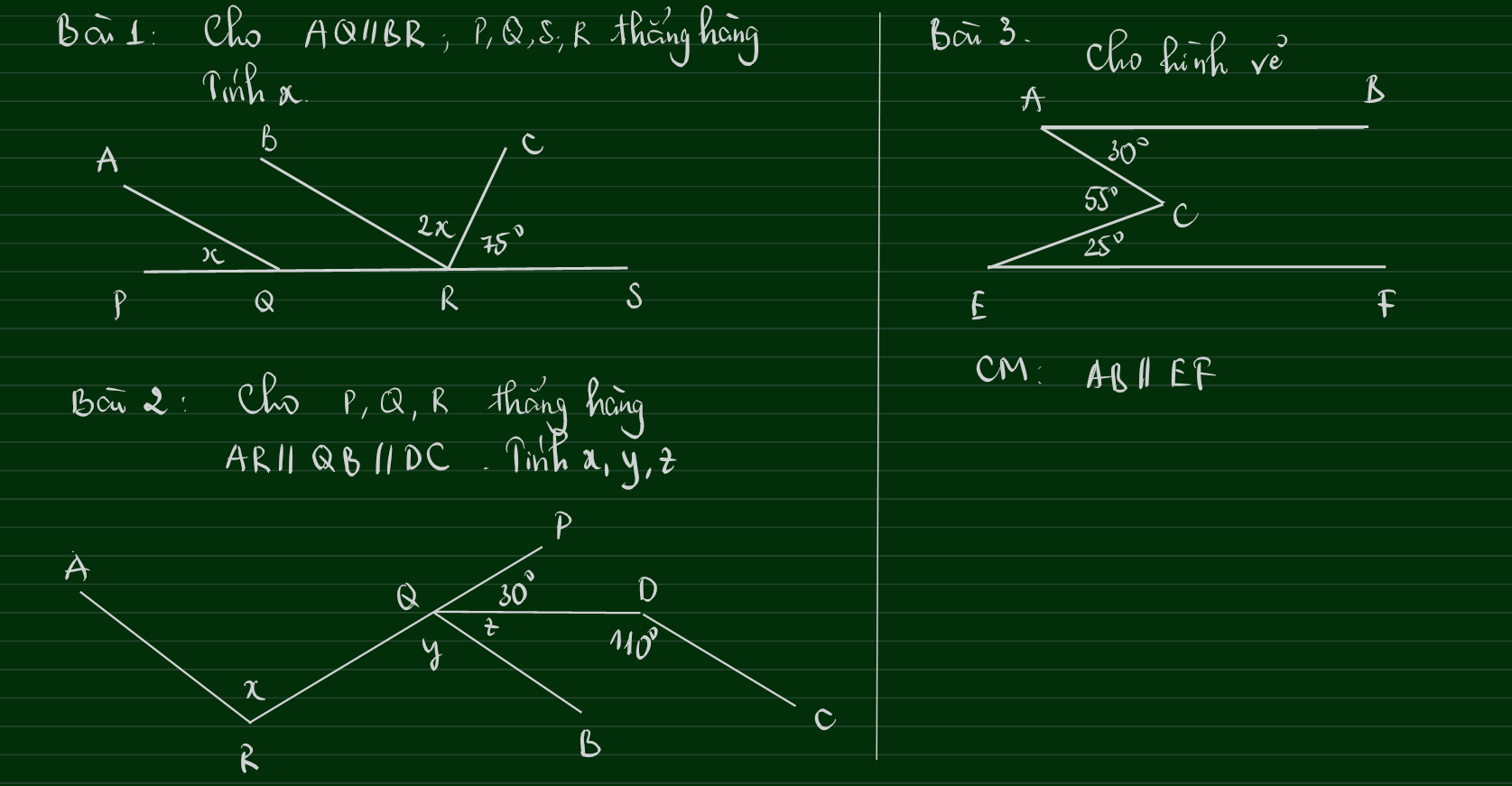
Bài 1:
Vì $AQ\parallel BR$ nên $\widehat{PQA}=\widehat{QRB}$ (hai góc đồng vị )
$\Rightarrow \widehat{QRB}=x$
Lại có:
$Q,R,S$ thẳng hàng nên
$\widehat{QRS}=180^0$
$\widehat{QRB}+\widehat{BRC}+\widehat{CRS}=180^0$
$x+2x+75^0=180^0$
$3x+75^0=180^0$
$x=35^0$
Bài 2:
Vì $QB\parallel DC$ nên: $\widehat{BQD}+\widehat{QDC}=180^0$ (hai góc trong cùng phía)
$z+110^0=180^0$
$z=70^0$
$P,Q,R$ thẳng hàng
$\Rightarrow \widehat{PQR}=180^0$
$\widehat{RQB}+\widehat{BQD}+\widehat{DQP}=180^0$
$y+z+30^0=180^0$
$y+70^0+30^0=180^0$
$y=80^0$
$AR\parallel QB$
$\Rightarrow x=y=80^0$ (hai góc so le trong)
Bài 3:
Kẻ $CM\parallel AB$ (như hình)
$CM\parallel AB\Rightarrow \widehat{MCA}=\widehat{BAC}=30^0$
$\widehat{MCE}=\widehat{ACE}-\widehat{MCA}=55^0-30^0=25^0$
Do đó: $\widehat{MCE}=\widehat{CEF}$ (cùng bằng $25^0$)
Hai góc này lại ở vị trí so le trong
$\Rightarrow CM\parallel EF$
Do đó:
$AB\parallel EF$ (cùng song song với $CM$)
Ta có đpcm.