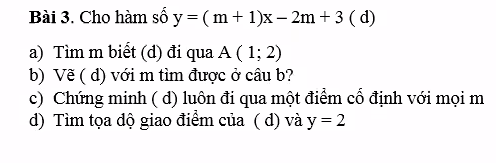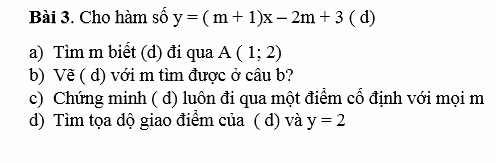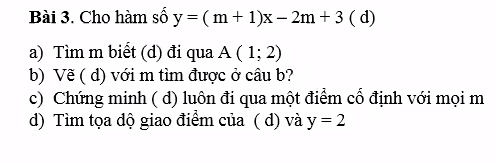a.
d đi qua A nên:
\(1\left(m+1\right)-2m+3=2\)
\(\Rightarrow m=2\)
b.
Em tự vẽ
c.
Giả sử điểm cố định mà d luôn đi qua là \(M\left(x_0;y_0\right)\), khi đó với mọi m ta luôn có:
\(y_0=\left(m+1\right)x_0-2m+3\)
\(\Leftrightarrow m\left(x_0-2\right)+x_0-y_0+3=0\)
\(\Rightarrow\left\{{}\begin{matrix}x_0-2=0\\x_0-y_0+3=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_0=2\\y_0=5\end{matrix}\right.\) \(\Rightarrow M\left(2;5\right)\)
d.
- Với \(m=-1\Rightarrow\) d không cắt y=2
- Với \(m\ne-1\)
\(\Rightarrow\left(m+1\right)x-2m+3=2\)
\(\Rightarrow\left(m+1\right)x=2m-1\)
\(\Rightarrow x=\dfrac{2m-1}{m+1}\)
Tọa độ giao điểm của d và y=2 là: \(\left(\dfrac{2m-1}{m+1};2\right)\)
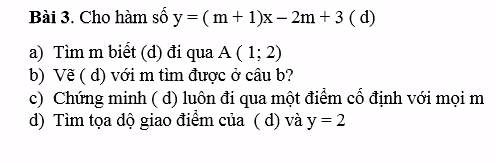
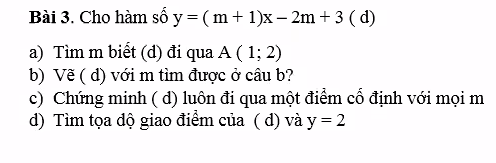Ạ,GIÚP EM VỚI Ạ
