c, Vì ME⊥AC và BA⊥AC
⇒ ME// AB (1)
Mà M là trung điểm của BC
⇒ E là trung điểm của AC
⇒ ME là đường TB của ΔABC
\(\Rightarrow ME=\dfrac{1}{2}AB\)
Chứng minh tương tự ta có: D là trung điểm của AB
⇒ DA=DB
⇒ ME=DA=DB (2)
Từ (1)(2) ⇒ BDEM là hình bình hành
Ta có:
AM=1/2MB(GT) ➪AM=MB
Xét tam giác AMB, ta có:
AM=MB ( CMT)
➪ Tam giác AMB là tam giác cân mà MD lại là đường cao của tam giác AMB( do MD┷ AB (GT))
➪ MD vừa là đường cao vừa là đường cao vừa là đường trung tuyến của tam giác AMB (T/C)
➪ DA=DB mà EM=AD ( do EMDA là hình chữ nhật (CM ở b))
➪ EM=DB (1)
Ta có:
ED=MA( do do EMDA là hình chữ nhật (CM ở b))
mà MA=MB (CMT)
➪MB=ED(2)
Từ (1) và (2)
➪ EMBD là hình bình hành (DHNB)













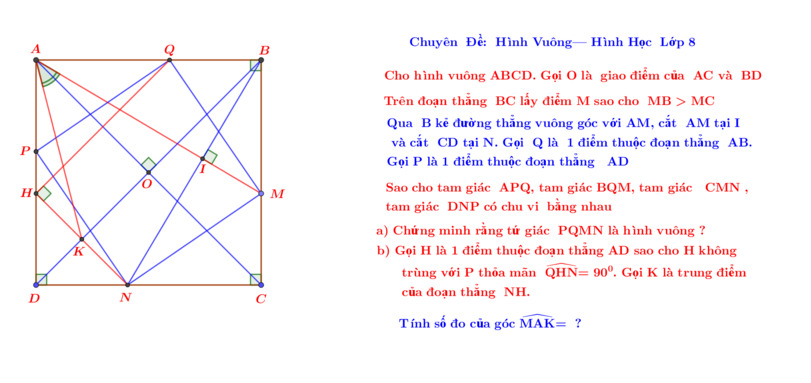
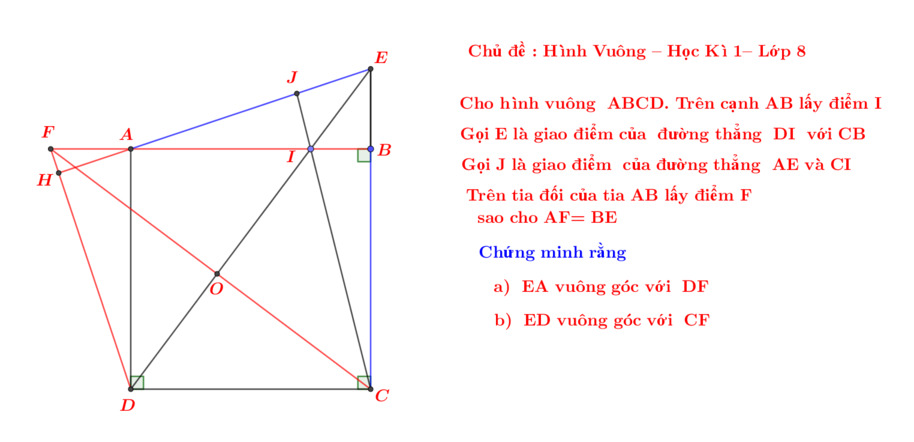
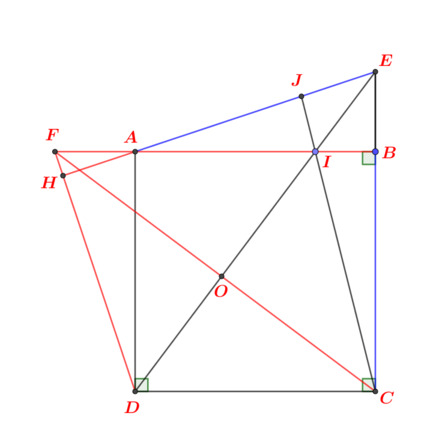






 Giải giúp em bài này với mọi người 😭
Giải giúp em bài này với mọi người 😭