Question

Giải giúp mình nha

Answer 1

-Hình vẽ:

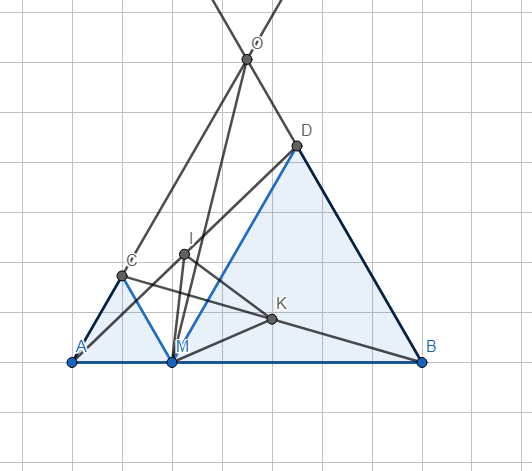
a) -Ta có: \(\widehat{CAM}=60^0\) (△ACM đều), \(\widehat{MBD}=60^0\) (△BDM đều).

=>\(\widehat{CAM}=\widehat{MBD}=60^0\) hay \(\widehat{OAB}=\widehat{OBA}=60^0\)

=>△ABO đều.

b) -Ta có: \(\widehat{AMC}=60^0\) (△ACM đều) ; \(\widehat{MBD}=60^0\) (△BDM đều).

=.\(\widehat{AMC}=\widehat{MBD}\) mà 2 góc này ở vị trí đồng vị.

=>MC//BO.

-Ta có: \(\widehat{CAM}=60^0\) (△ACM đều) ; \(\widehat{BMD}=60^0\) (△BDM đều).

=.\(\widehat{CAM}=\widehat{BMD}\) mà 2 góc này ở vị trí đồng vị.

=>AC//MD.

-Xét △OCM và △MDO có:

\(\widehat{OMC}=\widehat{MOD}\) (MC//OD và so le trong).

\(OM\) là cạnh chung.

\(\widehat{COM}=\widehat{DMO}\) (OC//MD và so le trong).

=>△OCM = △MDO (c-g-c).

=>\(MC=OD\) (2 cạnh tương ứng) ; \(MD=OC\) (2 cạnh tương ứng).

c) -Ta có: \(\widehat{BMD}+\widehat{AMD}=180^0\) (kề bù).

Mà \(\widehat{BMD}=60^0\) (△BDM đều).

=>\(60^0+\widehat{AMD}=180^0\)

=>\(\widehat{AMD}=120^0\)

-Ta có: \(\widehat{AMC}+\widehat{CMB}=180^0\) (kề bù).

Mà \(\widehat{AMC}=60^0\) (△ACM đều).

=>\(60^0+\widehat{CMB}=180^0\)

=>\(\widehat{CMB}=120^0\)

-Xét △AMD và △CMB có:

\(AM=CM\) (△ACM đều).

\(\widehat{AMD}=\widehat{CMB}=120^0\)

\(MD=MB\) (△BDM đều).

=>△AMD = △CMB (c-g-c).

=>\(AD=BC\) (2 cạnh tương ứng).

d) -Ta có: \(AD=2AI\) (I là trung điểm AD) ; \(BC=2CK\) (K là trung điểm BC).

Mà \(AD=BC\) (cmt) nên \(AI=CK\).

-Xét △AMI và △CMK có:

\(AI=CK\)(cmt).

\(\widehat{MAI}=\widehat{MCK}\)(△AMD = △CMB)

\(AM=CM\) (△ACM đều).

=>△AMI=△CMK (c-g-c).

=>\(MI=MK\) (2 cạnh tương ứng) nên △MIK cân tại M (1).

\(\widehat{AMI}=\widehat{CMK}\)(2 góc tương ứng).

Mà \(\widehat{AMI}=\widehat{AMC}+\widehat{CMI}\) ; \(\widehat{CMK}=\widehat{CMI}+\widehat{IMK}\)

=>\(\widehat{AMC}=\widehat{CMI}\).

Mà \(\widehat{AMC}=60^0\) (△AMC đều).

=>\(\widehat{CMI}=60^0\) (2).

-Từ (1) và (2) suy ra: △MIK đều.