Có x=a/m; y=b/m và x<y nên a/m<b/m ⇒a<b
Giả sử z>x là đúng thì\(\dfrac{a+b}{2m}>\dfrac{a}{m}\Leftrightarrow\dfrac{a+b}{2m}-\dfrac{a}{m}>0\\ \Leftrightarrow\dfrac{a+b-2a}{2m}>0\Leftrightarrow\dfrac{b-a}{2m}>0\\ m\text{à}b>a;m>0n\text{ê}nz>xl\text{à}\text{đ}\text{úng (1)}\)Giả sử z<y là đúng thì
\(\dfrac{a+b}{2m}< \dfrac{b}{m}\Leftrightarrow\dfrac{a+b}{2m}-\dfrac{b}{m}< 0\\ \Leftrightarrow\dfrac{a+b-2b}{2m}< 0\Leftrightarrow\dfrac{a-b}{2m}< 0\\ m\text{à}a< b;m>0n\text{ê}nz< yl\text{à}\text{đ}\text{úng (2)}\)
Từ (1)và(2) suy ra đpcm










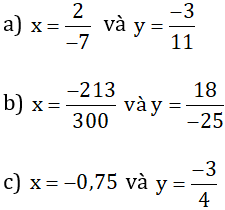
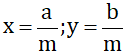 (a, b, m ∈ Z; m > 0) và x < y. Hãy chứng minh nếu chọn
(a, b, m ∈ Z; m > 0) và x < y. Hãy chứng minh nếu chọn 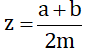 thì ta có x < z < y.
thì ta có x < z < y.
