Lời giải:
Đặt \(I=\int \frac{\sqrt{x^2-1}dx}{x^3}\)
Nguyên hàm từng phần:
Đặt \(\left\{\begin{matrix} u=\sqrt{x^2-1}\\ dv=\frac{1}{x^3}dx\end{matrix}\right.\Rightarrow \left\{\begin{matrix} du=\frac{x}{\sqrt{x^2-1}}dx\\ v=\frac{-1}{2x^2}\end{matrix}\right.\)
\(\Rightarrow I=\frac{-\sqrt{x^2-1}}{2x^2}+\int \frac{dx}{x\sqrt{x^2-1}}\)
Xét \(\int \frac{dx}{x\sqrt{x^2-1}}=\int \frac{d(x^2)}{2x^2\sqrt{x^2-1}}\). Đặt \(\sqrt{x^2-1}=t\rightarrow x^2=t^2+1\)
Khi đó, \(\int \frac{dx}{x\sqrt{x^2-1}}=\int \frac{d(t^2+1)}{2t(t^2+1)}=\int \frac{dt}{t^2+1}\)
Đặt \(t=\tan m\), đây là một dạng toán đặt quen thuộc, ta thu
được \(\int \frac{dx}{x\sqrt{x^2-1}}=\int \frac{dt}{t^2+1}=m=\tan ^{-1}t=\tan ^{-1}(\sqrt{x^2-1})\)
Do đó, \(\int \frac{\sqrt{x^2-1}dx}{x^3}=\frac{-\sqrt{x^2-1}}{2x^2}+\frac{1}{2}\tan ^{-1}(\sqrt{x^2-1})\)
\(\Rightarrow \int ^{\sqrt{2}}_{1}\frac{\sqrt{x^2-1}}{x^3}dx=\frac{\pi}{8}-\frac{1}{4}\)














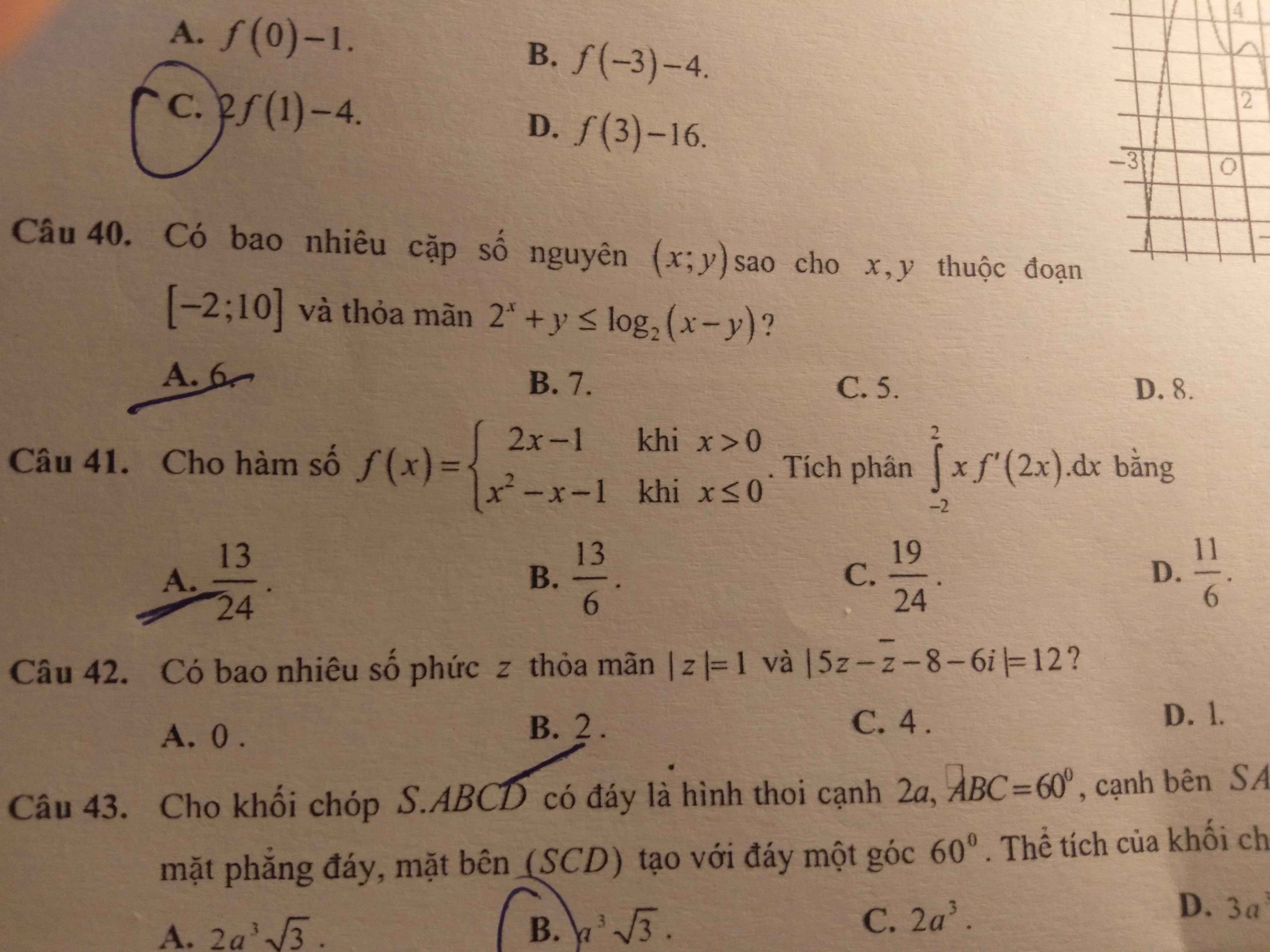


 giải giúp e câu 2,4,5,6 vs ạ.
giải giúp e câu 2,4,5,6 vs ạ.
