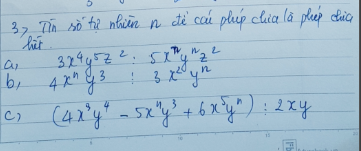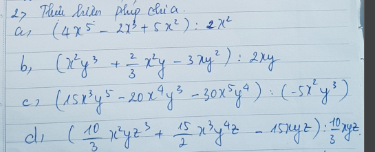Question

cứu em vs

Answer 1

\(1,=\left(3x^4-2x^3+x^2-6x^3+4x^2-2x-15x^2+10x-5\right):\left(3x^2-2x+1\right)\\ =\left(3x^2-2x+1\right)\left(x^2-2x-5\right):\left(3x^2-2x+1\right)\\ =x^2-2x-5\\ 2,=\left(x^4+x^2+2x^3+2x-x^2-1+8x-24\right):\left(x^2+1\right)\\ =\left[\left(x^2+1\right)\left(x^2+2x-1\right)+8x-24\right]:\left(x^2+1\right)\\ =x^2+2x-1\left(dư.8x-24\right)\\ 3,=\left(3x^4-8x^3-10x^2+8x-5\right):\left(3x^2-2x+1\right)\\ =x^2-2x-5\left(câu.1\right)\\ 4,=\left(x^3-5x^2-x^2+5x-3x+15\right):\left(x-5\right)\\ =\left(x-5\right)\left(x^2-x-3\right):\left(x-5\right)\\ =x^2-x-3\)

\(5,=\left(-12x^2+13x-5\right):\left(3x^2-2x+1\right)\\ =\left(-12x^2+8x+4+5x-9\right):\left(3x^2-2x+1\right)\\ =\left(3x^2-2x+1\right)\left(-4\right)-9\\ =-4\left(dư.-9\right)\\ 6,=\left(x^3+2x^2-5x^2-10x+12x+24\right):\left(x+2\right)\\ =\left(x+2\right)\left(x^2-5x+12\right):\left(x+2\right)\\ =x^2-5x+12\\ 7,=\left(2x^3-x^2+x+6x^2-3x+3\right):\left(2x^2-x+1\right)\\ =\left(2x^2-x+1\right)\left(x+3\right):\left(2x^2-x+1\right)\\ =x+3\\ 8,=\left(2x^3+4x^2-x^2-2x+x+2\right):\left(x+2\right)\\ =\left(x+2\right)\left(2x^2-x+1\right):\left(x+2\right)\\ =2x^2-x+1\)

\(9,=\left(9x^4-16x^2+4\right):\left(3x^2+2x-2\right)\\ =\left(9x^4+6x^3-6x^2-6x^3-4x^2+4x-6x^2-4x+4\right):\left(3x^2+2x-2\right)\\ =\left(3x^2+2x-2\right)\left(3x^2-2x-2\right):\left(3x^2+2x-2\right)\\ =3x^2-2x-2\\ 10,=\left(2x^3+4x^2-7x^2-14x+15x+30\right):\left(x+2\right)\\ =\left(x+2\right)\left(2x^2-7x+15\right):\left(x+2\right)\\ =2x^2-7x+15\)