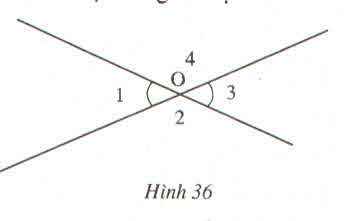
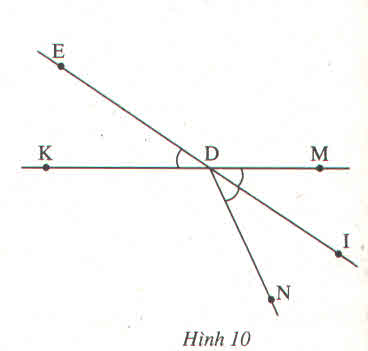
Hình vẽ:
\(GT:\) \(\widehat{xOy}\) và \(\widehat{x'Oy'}\) đối đỉnh
\(\widehat{mOx}=\widehat{mOy}=\dfrac{1}{2}\widehat{xOy}\)
\(\widehat{nOy'}=\widehat{nOx'}=\dfrac{1}{2}\widehat{x'Oy'}\)
\(KL:\widehat{mOn}=180^o\)
Chứng minh:
Ta có: \(\widehat{mOx}=\widehat{mOy}=\dfrac{1}{2}\widehat{xOy}\)(phân giác)
\(\widehat{nOx'}=\widehat{nOy'}=\dfrac{1}{2}\widehat{x'Oy'}\)(phân giác)
\(\widehat{xOy}=\widehat{x'Oy'}\)(đối đỉnh) nên \(\dfrac{1}{2}\widehat{xOy}=\dfrac{1}{2}\widehat{x'Oy'}\)
Vì \(Oy;Ox'\) nằm giữa \(Om\) và \(On\) nên:
\(\widehat{mOy}+\widehat{yOx'}+\widehat{nOx'}=\widehat{mOn}\)
\(\widehat{\widehat{mOn}=\dfrac{1}{2}\widehat{xOy}+\widehat{yOx'}+\dfrac{1}{2}\widehat{x'Oy'}}\)
\(\widehat{mOn}=\dfrac{1}{2}\widehat{xOy}+\widehat{yOx'}+\dfrac{1}{2}\widehat{xOy}\)
\(\widehat{mOn}=\widehat{xOy}+\widehat{yOx'}=180^o\)(kề bù)
Ta có đpcm