Question

Cho tứ giác ABCD có \(\widehat B = \widehat D = {90^o}\).

a) Chứng minh bốn điểm A, B, C, D cùng nằm trên một đường tròn.

b) So sánh độ dài của AC và BD.

Answer 1

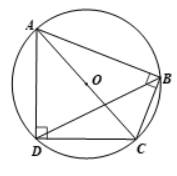
a) Gọi O là trung điểm của AC.

Xét tam giác ABC vuông tại B có O là trung điểm của AC nên \(OA = OB = OC = \frac{1}{2} AC\)

Xét tam giác ADC vuông tại D có O là trung điểm của AC nên \(OA = OD = OC = \frac{1}{2} AC\)

Suy ra \(OA = OB = OC = OD = \frac{1}{2} AC\) nên A, B, C, D cùng nằm trên một đường tròn tâm O đường kính AC.

b) Xét đường tròn tâm O đường kính AC có BD là dây cung không đi qua tâm O nên AC > BD.