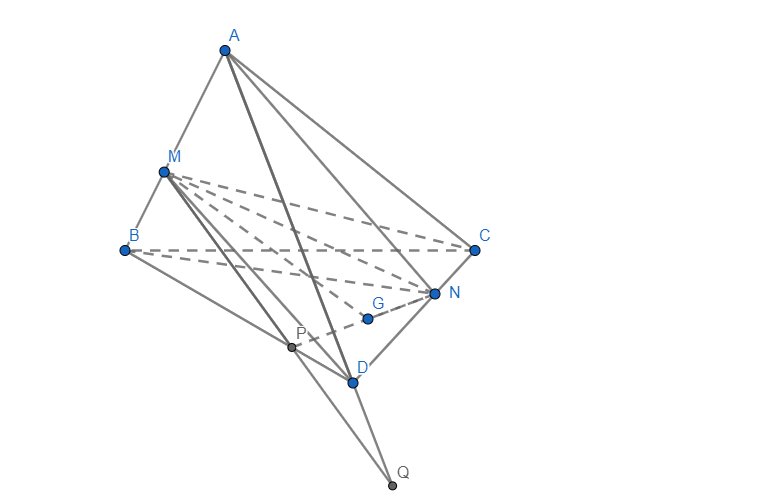
a) Ta có:
\(\left\{{}\begin{matrix}M\in\left(MCD\right)\\M\in AB\subset\left(NAB\right)\end{matrix}\right.\)\(\Rightarrow M\in\left(MCD\right)\cap\left(NAB\right)\)
\(\left\{{}\begin{matrix}N\in CD\subset\left(MCD\right)\\N\in\left(NAB\right)\end{matrix}\right.\)\(\Rightarrow N\in\left(MCD\right)\cap\left(NAB\right)\)
\(\Rightarrow MN=\left(MCD\right)\cap\left(NAB\right)\)
b) Trong mp(BCD), gọi \(P=NG\cap BD\)
Trong mp(BAD), gọi \(Q=PM\cap AD\)
Ta có:
\(\left\{{}\begin{matrix}N\in\left(GMN\right)\\N\in CD\subset\left(ACD\right)\end{matrix}\right.\)\(\Rightarrow N\in\left(GMN\right)\cap\left(ACD\right)\)
Ta có:
\(\left\{{}\begin{matrix}Q\in MP\subset\left(GMN\right)\\Q\in AD\subset\left(ACD\right)\end{matrix}\right.\)\(\Rightarrow Q\in\left(GMN\right)\cap\left(ACD\right)\)
\(\Rightarrow NQ=\left(GMN\right)\cap\left(ACD\right)\)