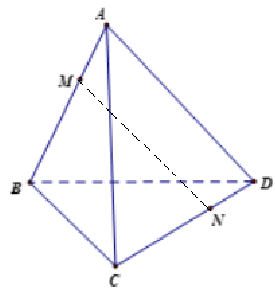
Ta có: \(\overrightarrow {MB} + 2\overrightarrow {MA} = \overrightarrow 0 \Rightarrow \overrightarrow {MB} = - 2\overrightarrow {MA} ,\overrightarrow {NC} = 2\overrightarrow {DN} \Rightarrow \overrightarrow {CN} = - 2\overrightarrow {DN} \)
Ta có: \(\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AD} + \overrightarrow {DN} \) (1)
\(\overrightarrow {MN} = \overrightarrow {MB} + \overrightarrow {BC} + \overrightarrow {CN} = - 2\overrightarrow {MA} + \overrightarrow {BC} - 2\overrightarrow {DN} \) (2)
Cộng vế với vế của (1) và (2) ta có:
\(2\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AD} + \overrightarrow {DN} - 2\overrightarrow {MA} + \overrightarrow {BC} - 2\overrightarrow {DN} = - \overrightarrow {MA} - \overrightarrow {DN} + \overrightarrow {BC} + \overrightarrow {AD} \)
\( = \frac{1}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {CD} + \overrightarrow {BC} + \overrightarrow {AD} = \frac{1}{3}\left( {\overrightarrow {AC} + \overrightarrow {CB} + \overrightarrow {CA} + \overrightarrow {AD} } \right) + \overrightarrow {BC} + \overrightarrow {AD} = \frac{2}{3}\overrightarrow {BC} + \frac{4}{3}\overrightarrow {AD} \)
\(\overrightarrow {MN} = \frac{1}{3}\overrightarrow {BC} + \frac{2}{3}\overrightarrow {AD} \)


