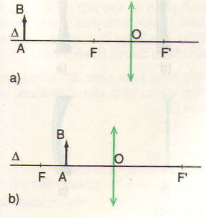
TH1, d=18cm<f=24cm nên ảnh A'B' trong Th này là ảnh ảo, cùng chiều với vật và lớn hơn vật.
Áp dụng công thức thấu kính hội tụ cho ảnh áo thì ta có
\(\dfrac{1}{f}=\dfrac{1}{d}-\dfrac{1}{d'}\Rightarrow d'=\dfrac{1}{\dfrac{1}{d}-\dfrac{1}{f}}=\dfrac{1}{\dfrac{1}{18}-\dfrac{1}{24}}=72\left(cm\right)\)
Mặt khác thì ta có, \(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow h'=\dfrac{d'.h}{d}=\dfrac{72.1}{18}=4\left(cm\right)\)
TH2 d=36cm>f=24cm nên ảnh A'B' của AB qua TKHT là ảnh thật, ngược chiều với vật và lớn hơn vật.
Ta có công thức TKHT cho ảnh thật
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow d'=\dfrac{1}{\dfrac{1}{f}-\dfrac{1}{d}}=72\left(cm\right)\)
Mặt khác ta có \(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow h'=\dfrac{d'.h}{d}=\dfrac{1.72}{36}=2\left(cm\right)\)