Question

Cho tam giác ABC vuông tại A có đường cao AH và \(\widehat{B}=\alpha\) (Hình 40).

a) Tỉ số \(\dfrac{HA}{HB}\) bằng

A. sinα.              B. cosα.              C. tanα.              D. cotα.

b) Tỉ số \(\dfrac{HA}{HC}\) bằng

A. sinα.              B. cosα.              C. tanα.              D. cotα.

c) Tỉ số \(\dfrac{HA}{AC}\) bằng

A. sinα.              B. cosα.              C. tanα.              D. cotα.

Answer 1

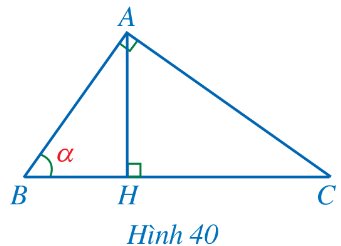
a) Chọn đáp án C.

b) Xét tam giác \(AHC\) vuông tại \(H\) có:

\(\tan C = \frac{{HA}}{{HC}}\).

Do \(\widehat B + \widehat C = 90^\circ \) nên \(\tan C = \cot B\).

Vậy \(\cot \alpha  = \frac{{HA}}{{HC}}\).

Chọn đáp án D.

c) Xét tam giác \(AHC\) vuông tại \(H\) có:

\(\sin C = \frac{{HA}}{{AC}}\).

Do \(\widehat B + \widehat C = 90^\circ \) nên \(\sin C = \cos B\).

Vậy \(\cos \alpha  = \frac{{HA}}{{AC}}\).

Chọn đáp án B.