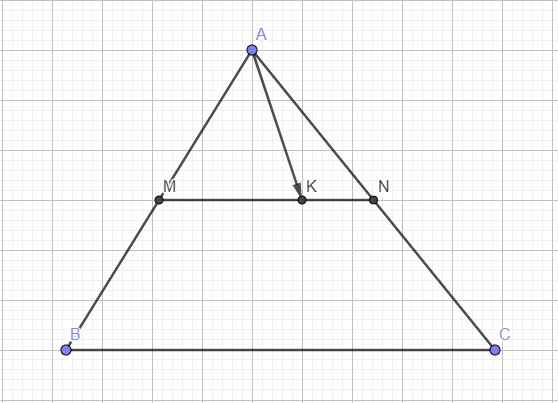
MN là đường trung bình của tam giác ABC
\(\Rightarrow\overrightarrow{MN}=\dfrac{1}{2}\overrightarrow{BC}=\dfrac{1}{2}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)=-\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\)
Từ giả thiết:
\(\overrightarrow{KM}=-2\overrightarrow{KN}=-2\left(\overrightarrow{KM}+\overrightarrow{MN}\right)\)
\(\Rightarrow3\overrightarrow{KM}=2\overrightarrow{NM}\Rightarrow\overrightarrow{KM}=\dfrac{2}{3}\overrightarrow{NM}\)
\(\Rightarrow\overrightarrow{MK}=\dfrac{2}{3}\overrightarrow{MN}=\dfrac{2}{3}\left(-\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)=-\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)
M là trung điểm AB \(\Rightarrow\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB}\)
Do đó:
\(\overrightarrow{AK}=\overrightarrow{AM}+\overrightarrow{MK}=\dfrac{1}{2}\overrightarrow{AB}-\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}=\dfrac{1}{6}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)