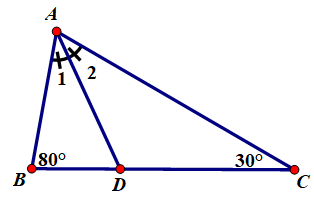
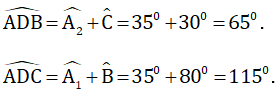Áp dụng định lý góc ngoài trong các tam giác ABD và ACD ta có:
Chúc bạn học tốt!
+ Xét \(\Delta ABC\) có:
\(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\) (định lí tổng 3 góc trong một tam giác).
=> \(\widehat{BAC}+80^0+30^0=180^0\)
=> \(\widehat{BAC}+110^0=180^0\)
=> \(\widehat{BAC}=180^0-110^0\)
=> \(\widehat{BAC}=70^0.\)
+ Vì \(AD\) là tia phân giác của \(\widehat{BAC}\left(gt\right)\)
=> \(\widehat{BAD}=\widehat{CAD}=\frac{\widehat{BAC}}{2}.\)
=> \(\widehat{BAD}=\widehat{CAD}=\frac{70^0}{2}=35^0.\)
+ Xét \(\Delta ABD\) có:
\(\widehat{ABD}+\widehat{BAD}+\widehat{ADB}=180^0\) (định lí tổng 3 góc trong một tam giác).
=> \(80^0+35^0+\widehat{ADB}=180^0\)
=> \(115^0+\widehat{ADB}=180^0\)
=> \(\widehat{ADB}=180^0-115^0\)
=> \(\widehat{ADB}=65^0.\)
+ Xét \(\Delta ACD\) có:
\(\widehat{ACD}+\widehat{CAD}+\widehat{ADC}=180^0\) (định lí tổng 3 góc trong một tam giác).
=> \(30^0+35^0+\widehat{ADC}=180^0\)
=> \(65^0+\widehat{ADC}=180^0\)
=> \(\widehat{ADC}=180^0-65^0\)
=> \(\widehat{ADC}=115^0.\)
Vậy \(\widehat{ADC}=115^0;\widehat{ADB}=65^0.\)
Chúc bạn học tốt!
Hình tự vẽ.
Xét TG ABC có:
góc A + B + C = 180o (theo tính chất tổng 3 góc của TG)
hay góc A + 80o + 30o = 180o
Suy ra góc A = 70o
Do AD là phân giác góc A
suy ra góc BAD = CAD = \(\frac{1}{2}A\) = \(\frac{1}{2}70^{o^{ }}\) = 35o
Xét TG ABD có:
góc B + ADB + BAD = 180o (theo t/c tổng 3 góc của TG)
hay 80o + ADB + 35o = 180o
suy ra góc ADB = 65o
mà 2 góc ADB và ADC kề bù
Suy ra ADC = 180o - ADB = 180o-65o = 115o