Ta có: \(M=a^3+b^3+c\left(a^2+b^2\right)-abc\)
\(M=\left(a+b\right)\left(a^2-ab+b^2\right)+c\left(a^2+b^2-ab\right)\)
\(M=\left(a+b+c\right)\left(a^2+b^2-ab\right)\)
\(M=0.\left(a^2+b^2-ab\right)\)
\(M=0\)
Vậy \(M=0\)
BÀI 3: Cho biểu thức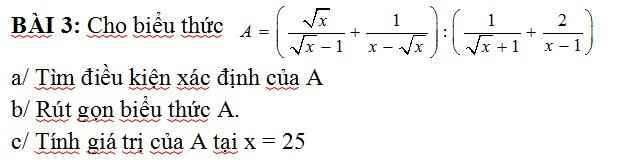 
a/ Tìm điều kiện xác định của A
b/ Rút gọn biểu thức A.
c/ Tính giá trị của A tại x = 25
cho biểu thức
P=\(\dfrac{1}{\sqrt{x}+1}+\dfrac{x}{\sqrt{x}-x}\)
a. rút gọn P
b.tính gtri biểu thức P khi x=\(\dfrac{1}{\sqrt{2}}\)
1. Cho biểu thức: A=\(\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{3\sqrt{x}}{x+\sqrt{x}}+\dfrac{6\sqrt{x}-4}{1-x}\)
Rút gọn biểu thức trên
1. Cho biểu thức: A=\(\left(\sqrt{x}+\dfrac{4\sqrt{x}}{\sqrt{x}-2}\right):\left(\dfrac{\sqrt{x}}{\sqrt{x}-2}+\dfrac{4}{2\sqrt{x}-x}\right)\)
Rút gọn biểu thức trên
1. Cho biểu thức: A=\(\left(\dfrac{\sqrt{x}}{x-\sqrt{x}}-\dfrac{2}{x\sqrt{x}-x+\sqrt{x}-1}\right):\left(1-\dfrac{\sqrt{x}}{x+1}\right)\)
Rút gọn biểu thức trên
cho A = \(\dfrac{\sqrt{x}+4}{\sqrt{x}+2x}\) và B = \(\dfrac{\sqrt{x}}{x-4}-\dfrac{2}{\sqrt{x}-2}\)
a, tính giá trị của biểu thức A khi x = 36
b, rút gọn biểu thức P = B : A
1.Cho biểu thức A=\(\dfrac{x^2+\sqrt{x}}{x-\sqrt{x}+1}-\dfrac{2x+\sqrt{x}}{\sqrt{x}}+1\)
a, rút gọn biểu thức
b, Tìm x để A có giá trị bằng 0
Rút gọn biểu thức: \(\sqrt{x}-\sqrt{x-\sqrt{x}+\dfrac{1}{4}}\) khi \(x\ge0\)
rút gọn biểu thức
\(\dfrac{5+2\sqrt{5}}{\sqrt{5}}-\dfrac{1}{\sqrt{5}-2}\)
Cho biểu thức P = \(\left(\dfrac{4a}{\sqrt{a}-1}-\dfrac{\sqrt{a}}{a-\sqrt{a}}\right).\dfrac{\sqrt{a}-1}{a^2}\) với a>0 và a \(\ne\)1
a)Rút gọn biểu thức P b)Với giá trị nào của a thì P = 3
